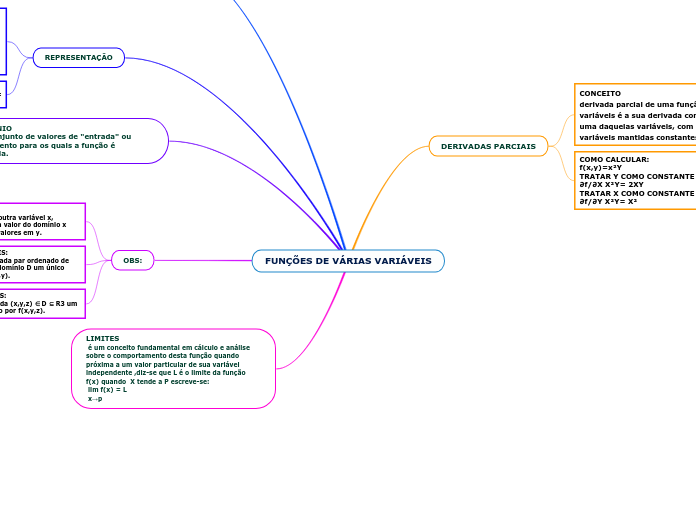
FUNÇÕES DE VÁRIAS VARIÁVEIS
DERIVADAS PARCIAIS
CONCEITO
derivada parcial de uma função de várias variáveis é a sua derivada com respeito a uma daquelas variáveis, com as outras variáveis mantidas constantes.
COMO CALCULAR:
f(x,y)=x²Y
TRATAR Y COMO CONSTANTE
∂f/∂X X²Y= 2XY
TRATAR X COMO CONSTANTE
∂f/∂Y X²Y= X²
CONCEITO
Função matemática é uma relação entre dois conjuntos quaisquer, que associa a cada elemento de partida denominada domínio, a único elemento de um conjunto de chegada denominado, contra- domínio.
REPRESENTAÇÃO
EXPRESSÃO MATEMÁTICA
uma função f que a cada ponto t de um conjunto
A associa um ponto f(t) de um conjunto B é dado por:
f: A=B
t= f(t)
neste caso, A é o domínio e B é o contra- domínio de f.
GRÁFICO
uma função f é o subconjunto do plano xy dado por:
G={(x,y)∈ R²: y=f(x)}
DOMÍNIO
é o conjunto de valores de "entrada" ou argumento para os quais a função é definida.
OBS:
FUNÇÃO DE UMA VARIÁVEL:
uma variável y é função de outra variável x, quando y = f(x), isto é, cada valor do domínio x corresponde a um ou mais valores em y.
FUNÇÃO DE DUAS VARIÁVEIS:
é uma regra que associa a cada par ordenado de números reais (x,y) de um domínio D um único valor real, denotado por f(x,y).
FUNÇÃO DE TRÊS VARIÁVEIS:
associa a cada tripla ordenada (x,y,z) ∈ D ⊆ R3 um único número real, denotado por f(x,y,z).