Geometria analitica

Las figuras geométricas

mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas.

Es un conjunto de puntos que cumplen determinadas condiciones o propiedades geométricas

EN EL PLANO

MEDIATRIZ

es el lugar geométrico de los puntos del plano que equidistan de los extremos

BISECTRIZ

Bisectriz de un ángulo es el lugar geométrico de los puntos del plano que equidistan de las rectas que forman el ángulo.

EQUIDISTANCIA A DOS RECTAS

la paralela media es el lugar geométrico de los puntos que las equidistan.

SECCIONES CÓNICAS

es el lugar geométrico de los puntos de un plano que equidistan a otro punto llamado centro.

Una sección cónica es la intersección de un plano y un cono.

CIRCUNFERENCIA

es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro.

Determinada cuando conocemos tres puntos de la misma, equidistantes del centro.

El centro y el radio.

El centro y un punto en ella.

El centro y una recta tangente a la circunferencia.

La ecuación ordinaria es

(x ─ a) 2 + (y ─ b) 2 = r 2

ELIPSE

a sección producida por un plano que interseca a todas las generatrices de un mismo lado del vértice es una elipse

los focos son los puntos de coordenadas F1(–c,0) y F2(c,0) y el punto medio entre los focos, se denomina centro C(0,0).

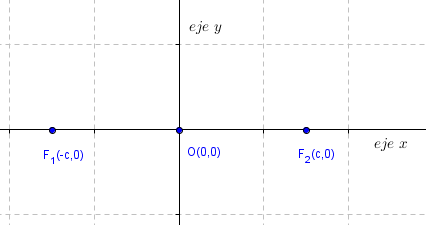
Dados dos puntos F1 y F2 llamados focos, se denomina elipse al conjunto de puntos del plano tales que la suma de sus distancias a ambos focos es constante

PARÁBOLA

La sección producida por un plano paralelo a una de las generatrices es una parábola.

El eje focal es el eje perpendicular a la directriz que pasa por el foco. Es el eje de simetría de la parábola.

El punto de la parábola que pertenece al eje focal se llama vértice

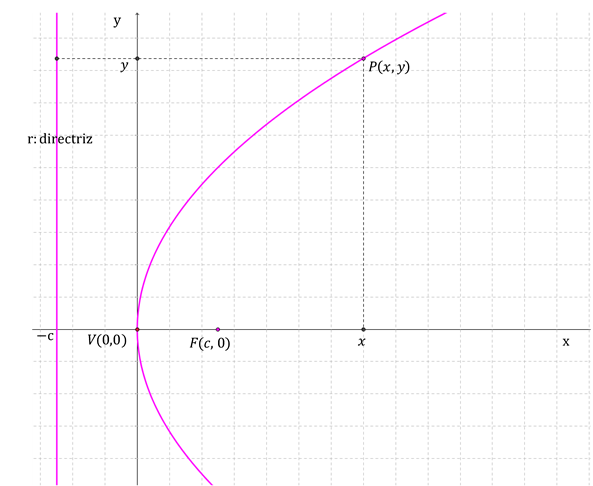
Dados un punto F (foco) y una recta r (directriz), se denomina parábola al conjunto de puntos del plano que equidistan del foco y de la directriz.

HIPÉRBOLE

La seccion producida por un plano que interdeca a todas las generatrices pero no en un mismo lado del vertice es una hiperbola.

Dados dos puntos F1 y F2 llamados focos, se denomina hipérbola al conjunto de puntos del plano tales que el valor absoluto de la diferencia de sus distancias a los focos es constante.

Matemáticas

Topografía

Ingeniería

Astronomía

René Descartes

Por el apéndice La Géométrie incluido en su Discurso del método, publicado en 1637.

Donde propone la idea de unión del álgebra y de la geometría en una sola disciplina y dio nacimiento a la geometría analítica, que permite la expresión de las formas geométricas en ecuaciones algebraicas y viceversa.

Pierre de Fermat

Conocía y utilizaba el método antes de su publicación por Descartes.

Frans van Schooten

Se atribuye su ampliación, desarrollo y divulgación en el mundo matemático.

Omar Khayyam

Ya en el siglo XI, utilizó un método muy parecido para determinar ciertas intersecciones entre curvas.

Está formado por dos rectas numéricas perpendiculares, una horizontal y otra vertical que se cortan en un punto.

El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados .

P (x, y)

Localizar el punto A (-4, 5) en el plano cartesiano.

El punto A se ubica 4 lugares hacia la izquierda en la abcisa (x) y 5 lugares hacia arriba en ordenada (y).

Otra de las utilidades radica en que, a partir de la ubicación de las coordenadas de dos puntos es posible calcular la distancia entre ellos.

La pendiente

es la inclinación de la recta con respecto al eje de abscisas.

LINEA RECTA

es una línea recta infinita: no tiene ningún límite.

también podemos limitarla con dos extremos, de modo que pasa de ser una recta a ser un segmento de recta

PUNTO DE DIVISIÓN

Es dividir un segmento AB en una relación dada r es

determina un punto P de la recta que contiene al segmento AB, de modo que las dos partes, PA y PB, están en la relación r: