GEOMETRÍA PLANA
CAPÍTULO 1
FUNDAMENTOS MATEMÁTICOS
Y GEOMÉTRICOS
Proposición
Proposición simple:
Enunciado formado por una sola proposición.
Proposición compuesta:
Enunciado formado por dos o más proposiciones simples.
Axioma
Proposición que siendo evidente, no requiere demostración.
Postulado
Proposición que, aunque no tiene evidencia de axioma,
se admite sin demostración. Son propiedades geométricas
Ejemplos:
1. Por un punto pasan infinitas rectas.
2. Una recta es un conjunto ordenado de puntos, no existe primero ni último.
3. Por dos puntos pasa una sola recta.
Entre otros
Teorema
Proposición que es necesaria demostrar utilizando definiciones, axiomas o postulados.
Corolario
Proposición que es consecuencia directa de un teorema, cuya demostración requiere poco o ningún razonamiento.
Problema
Proposición que parte de ciertos datos para obtener un resultado, éstos pueden ser gráficos y/o numéricos, tanto los datos como los resultados

CONJUNTO DE LOS NÚMEROS REALES
AXIOMAS DE LOS NÚMEROS REALES
Axiomas de la Igualdad
Axioma Dicotomía
∀ a, b ∈ R
a = b ∨ a ≠ b
Axioma Reflexivo
∀ a, b ∈ R
a = a
Axioma Simétrico
∀ a, b ∈ R
a = b → b = a
Axioma Transitivo
∀ a, b, c ∈ R
a = b ∧ b = c → a = c
Axioma Aditivo
∀ a, b, c ∈ R
a = b → a + c = b + c
Axioma Multiplicativo
∀ a, b, c ∈ R
a = b → a * c = b * c
Axioma Cancelativo
∀ a, b, c ∈ R
a + c = b + c → a = b
Axiomas de la Adición y Multiplicación
Axioma Clausurativo - Unívoco
∀ a, b, c ∈ R
a + b = c
a * b = c
Axioma Asociativo
∀ a, b, c ∈ R
a + (b + c) = (a + b) + c
a * (b * c) = (a * b) * c
Axioma Modulativo
∀a, δ0: a + 0 = 0 + a = a
∀a, δ1: a * 1 = 1 * a = a
Axioma Invertivo
∀ a ∃ (-a): a + (-a) = 0
∀ a ∃ (1/a): a * (1/a)=1; a ≠ 0
Axioma Conmutativo
∀ a, b, c ∈ R
a + b = b + a
a * b = b * a
Axioma Distributivo - Recolectivo
∀ a, b, c ∈ R
a * (b + c) = a*b + a*c
Axiomas de Orden
Axioma Tricotomía
∀ a, b, c ∈ R
a ≠ b → a > b ∨ a < b
Axioma Antisimétrico
∀ a, b ∈ R
a > b → b ≯ a
Axioma Transitivo
∀ a, b, c ∈ R
a > b ∧ b > c → a > c
Axioma Aditivo
∀ a, b, c ∈ R
a > b → a + c > b + c
a < b → a + c < b + c
Axioma Multiplicativo
∀ a, b, c ∈ R; c ≠ 0
c < 0 ∨ c > 0: a > b → a * c > b * c
CAPÍTULO 2
DEFINICIONES GEOMÉTRICAS
BÁSICAS
Punto

Elemento geométrico que tiene
posición pero no dimensión.
Recta

Conjunto infinito de puntos
que siguen una misma dirección.
Semirecta

Es la parte de una recta que
tiene punto inicial pero no final.
Rayos

Son aquellos que pertenecen
a una misma recta, pero con
sentidos opuestos.
Plano
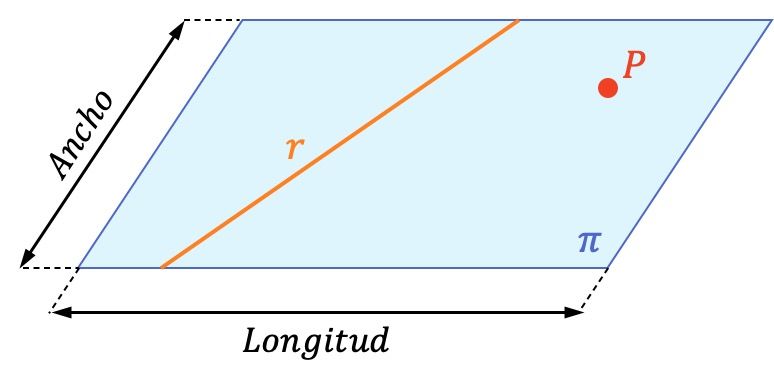
Conjunto infinito de puntos que
tiene dos dimensiones: largo y
ancho.
Espacio

Conjunto infinito de puntos que
tiene tres dimensiones: largo, ancho
y altura.
Sólido
Es un espacio limitado cualquiera por
tres dimensiones.
POSICIÓN RELATIVA ENTRE
PUNTO - RECTA, PUNTO - PLANO
Puntos colineales

Son todos los puntos elementos
de una recta
Puntos no colineales

Son todos los puntos que
no son elementos de un recta
Puntos coplanares

Son todos los puntos que pertenecen
a un plano
Puntos no coplanares
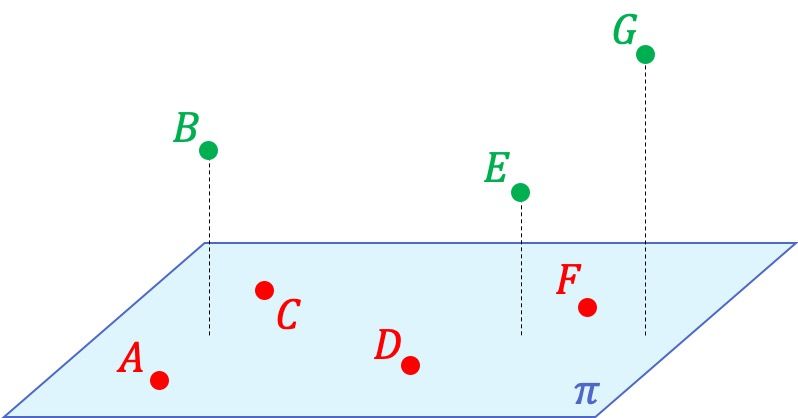
Son aquellos puntos que no son
elementos o no pertenecen a un plano
POSICIÓN RELATIVA DE LA RECTA
EN UN PLANO
Rectas paralelas

Son aquellas rectas que no se intersecan
Rectas secantes
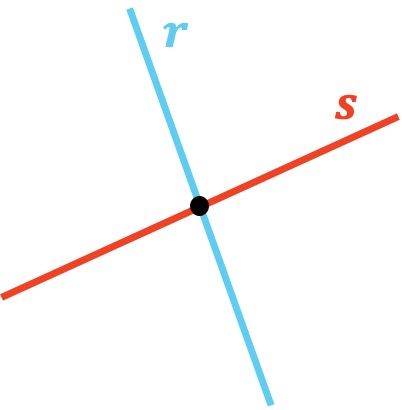
Dos rectas son secantes si y solo si,
su intersección es un punto
Rectas perpendiculares
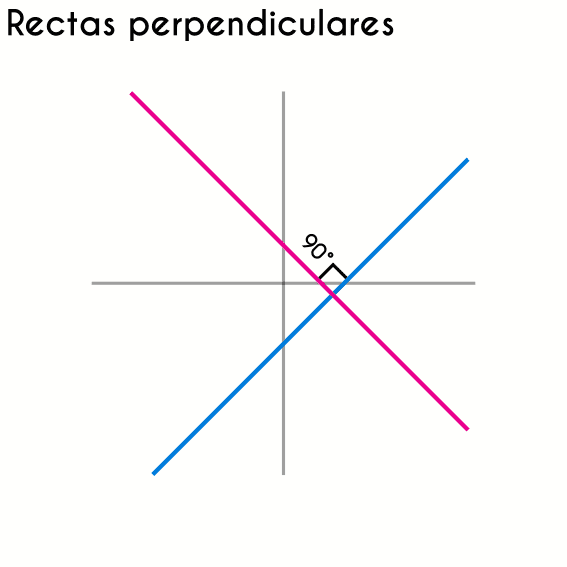
Dos rectas son perpendiculares, si
su intersección forma un ángulo de 90°
FIGURAS GEOMÉTRICAS
ELEMENTALES
Segmento

Es la figura geométrica de puntos colineales
cuyos elementos son A y B, y todos aquellos
entre A y B.
Segmento abierto

Figura geométrica de puntos colineales
cuyos elementos están comprendidos entre
A y B.
Segmento semiabierto

Figura geométrica de puntos colineales
cuyos elementos están comprendidos entre
A y B, incluyendo al punto A o B.
RELACIÓN ENTRE LAS
FIGURAS GEOMÉTRICAS
Congruencia
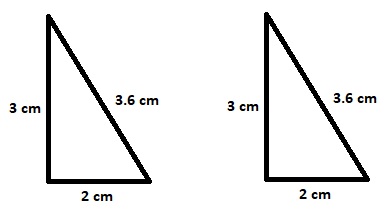
Dos figuras geométricas son congruentes
si tienen la misma forma, medida y al
superponerlas, sus puntos coinciden.
Semejanza

Dos figuras geométricas son semejantes si
tienen sus ángulos respectivamente
congruentes y sus lados proporcionales.