Grafos
Tipos de Grafo
Grafo Simple

Multigrafo o Pseudografo

Grafo Dirigido

Grafo Etiquetado

Grafo Aleatorio

Hipergrafo

Grafo Infinito

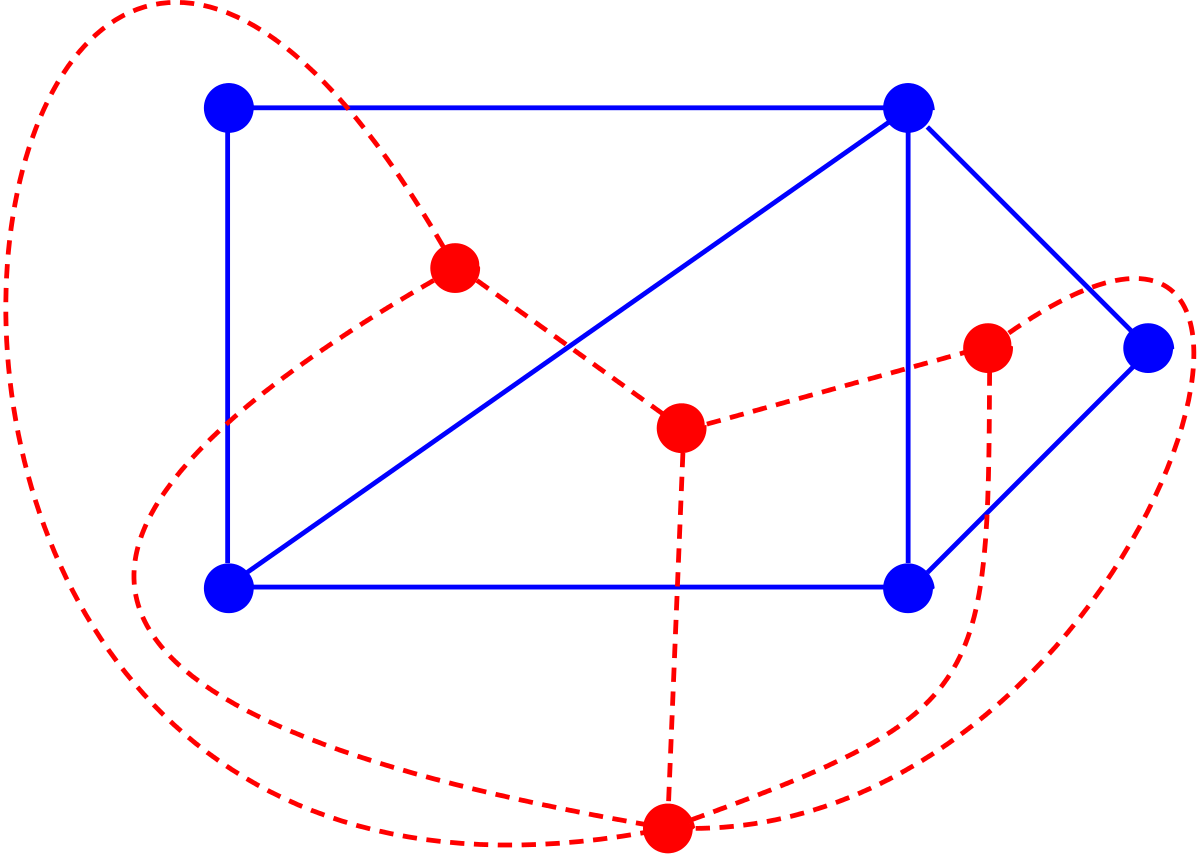
Grafo Plano

Grafo Regular

Grafo Dual
Estructura de Lista
Lista de Incidencia
El grafo está representado por una matriz de A (aristas) por V (vértices), donde [arista, vértice] contiene la información de la arista (conectado o no conectado).
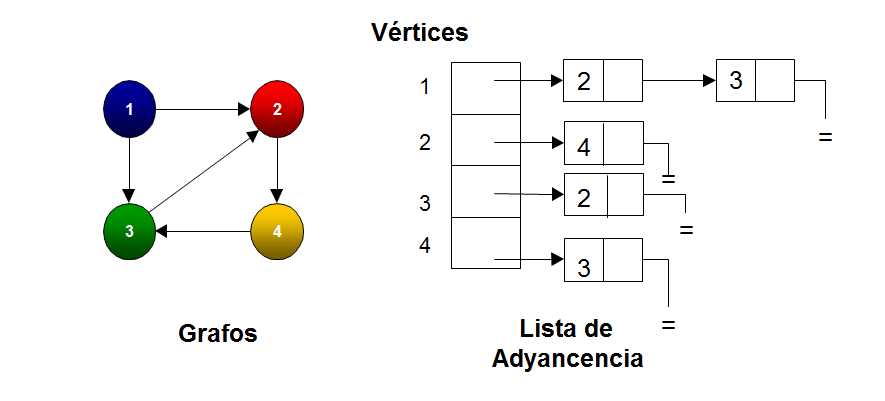
Lista de Adyacencia
El grafo está representado por un arreglo de listas de adyacencia. Para un vértice i, la lista de adyacencia está formada por todos los vértices adyacentes a i. Puede construirse en tiempo lineal, y las inserciones pueden hacerse al principio de cada lista, con lo que se asegura tiempo constante.
Lista de grados
También llamada secuencia de grados o sucesión gráfica de un una secuencia de números, que corresponde a los grados de los vértices del grafo.

Un grafo es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto. Se representa como una pareja de conjuntos G=(V, A), donde V es el conjunto de vértices, y A es el conjunto de aristas.
Propiedades
Adyacencia
En esta dos aristas son adyacentes si tienen un vértice en común, y dos vértices son adyacentes si una arista los une.
Incidencia
Una arista es incidente a un vértice si ésta lo une a otro.
Ponderación
Corresponde a una función que a cada arista le asocia un valor (costo, peso, longitud, etc.), para aumentar la expresividad del modelo. Esto se usa mucho para problemas de optimización, como el del vendedor viajero o del camino más corto.
Etiquetado
Es la distinción que se hace a los vértices y/o aristas mediante una marca que los hace unívocamente distinguibles del resto.
Estructura Matriciales
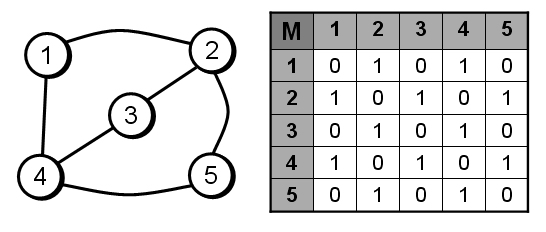
Matriz de Adyacencia
El grafo está representado por una matriz cuadrada M de tamaño n^2, donde n es el número de vértices. Si hay una arista entre un vértice x y un vértice y, entonces el elemento m_ {x, y} es 1, de lo contrario, es 0
Matriz de Incidencia
El grafo está representado por una matriz de A (aristas) por V (vértices), donde [vértice, arista] contiene la información de la arista (1 - conectado, 0 - no conectado)

Aplicaciones en la vida real

Ruta de Viaje

Conexión de Redes

Llamadas Teléfonicas