INTEGRALES
DEFINCIÓN: una función F(x) es antiderivada
de f(x) si F'(x)=f(x) para cada x en el dominio de la función.
![INTEGRAL DEFINIDA: APLICA PARA UNA FUNCIÓN CONTÍNUA DEFINIENDO SUS LIMITES SUPERIOR E INFERIOR [A,B]](https://i.ytimg.com/vi/wuI5MFhvgsY/maxresdefault.jpg)
INTEGRAL DEFINIDA: APLICA PARA UNA FUNCIÓN CONTÍNUA DEFINIENDO SUS LIMITES SUPERIOR E INFERIOR [A,B]

Por partes: usamos éste método cuando observamos una multiplicación de dos funciones, usamos la fórmula; Ejemplo: ∫(xe^x)dx; donde u=x, v=e^x,du=dx, Entonces= x.e^x-∫(e^x).dx
INTEGRALES TRIGONOMÉTRICAS: usamos identidades trigonométricas dependiendo del caso.
Funciones con potencia par, se usa la identidad del ángulo medio: Ejemplo: ∫cos^6dx
Una potencia par y otra impar: Ejemplo:
∫(sin^6xcos^3x)dx
Ambas potencias son pares y se usa la identidad del ángulo medio:
Ejemplo: ∫(sec^4xtan^2x)dx
SUSTITUCIÓN TRIGONOMÉTRICA
* a es positiva y bx^2 es negativa. Se usa:
x=(a/b)Sin♀; sin♀=bx/a; Ejemplo:∫√(4-2x²)dx
* a es positiva y bx^2 es positiva. Se usa:
x=(a/b)Tan♀; Tan♀=bx/a; Ejemplo:∫x√(x²+4)dx
* a es negativa y bx^2 es positiva. Se usa:
x=(a/b)Sec♀; Sec♀=bx/a; Ejemplo:∫dx/x²√(16x²-9)dx
APLICACIONES: problemas de valor inicial, valor promedio y variación
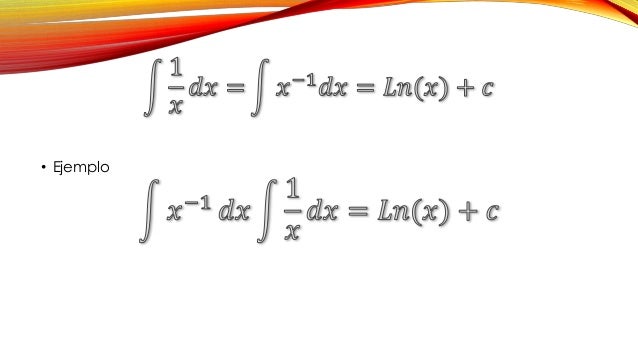
DIRECTA: usamos la definición para resolverla. Ejemplo:

SUSTITUCIÓN SIMPLE: se usa un cambio de variable para obtener una integral mas sencilla. Ejemplo:
Integración por Fracciones parciales: se encarga de resolver funciones racionales del tipo ∫[P(x)/Q(x)]dx. Se presentan varios casos:
CASO 2-EL DENOMINADOR CONTIENE FACTORES CUADRÁTICOS DISTINTOS:
(A1x + B1/a1x^2+b1x+c1)+...+(Anx+Bn/anx^2+bnx+cn)
CASO 1-EL DENOMINADOR CONTIENE FACTORES CUADRÁTICOS REPETIDOS:
(A1x + B1/a1x^2+b1x+c1)+(A2x+B2/a1x^2+b1x+c1)^2+...+(Anx+Bn/a1x^2+b1x+c1)^n
