Secciones Cónicas
En geometría existen un tipo de curvas planas llamadas cónicas, con el paso del tiempo se han convertido en una herramienta para descubrir y explicar acontecimientos relacionados con la astronomía, la óptica entre otras. Las secciones cónicas son todas las curvas obtenidas al cortar un cono de dos ramas con un plano, las diferentes posiciones representan diferentes curvas. Siendo a: Ángulo de conicidad, b: La inclinación del plano respecto al eje del cono.
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0


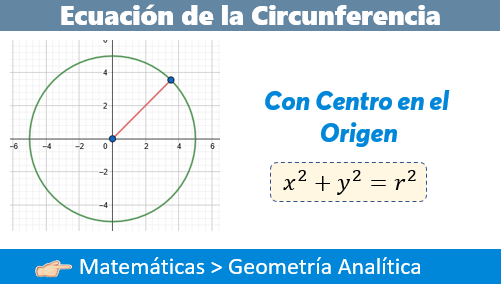
Circunferencia
Es el lugar geométrico o curva de un punto que se mueve en un plano de tal manera que se conserva siempre a una distancia constante a un punto fijo.
-A la distancia constante se le llama radio.
-Al punto fijo se le llama centro.
-El diámetro es el doble del radio y atraviesa la circunferencia.

Subtopic
Parábola
Es un lugar geométrico de un punto que se mueve en un plano de tal manera que su distancia de una recta fija, es siempre igual a su distancia de un punto fijo que no pertenece a la recta.
Según su posición se obtiene:
β = 90º el plano es paralelo a la base del cono entonces se obtiene una circunferencia.
β = α el plano es paralelo a una generatriz y corta a todas las demás se obtiene una parábola.
β > α la curva es una elipse.
β < α cortara las dos ramas del cono formando así la hipérbole.
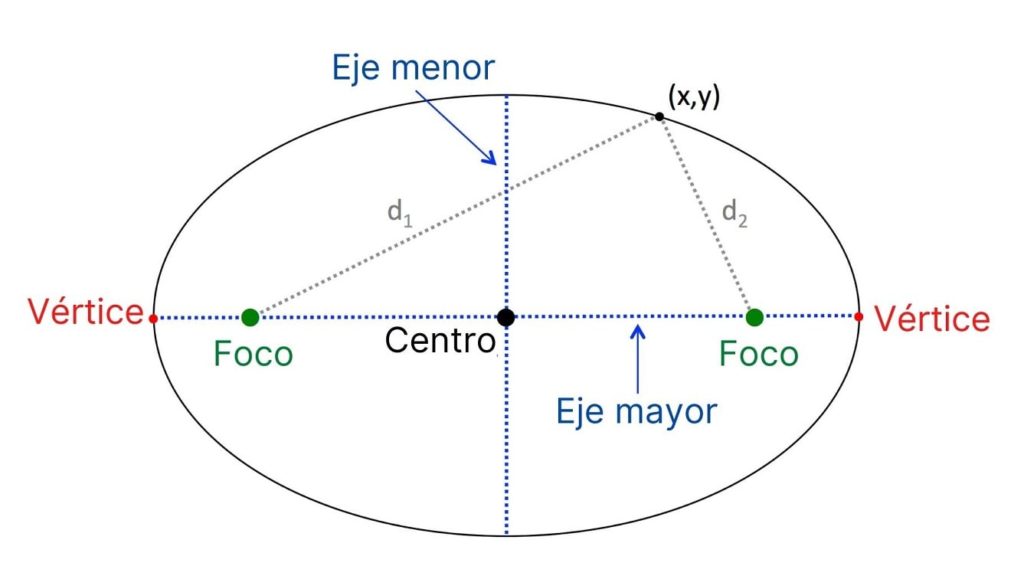
Elipse
Es el lugar geométrico de un punto que se mueve en un plano de tal manera que la suma de sus distancias a dos puntos fijos es siempre igual a una constante.
-Los puntos fijos se llaman focos, a la recta que pasa por los focos F y F1 se le denomina eje focal.
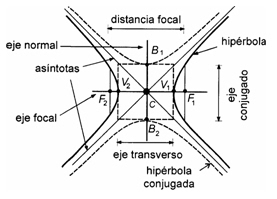
Hipérbola
Es el lugar geométrico de un punto que se mueve en un plano de tal manera que el valor absoluto de la diferencia de sus distancias a dos puntos fijos llamados focos es siempre constante y menos que la distancia entre los focos.
Topic principal
Ecuación Canonica V (0,0)

Eje de simetría "X"
y2=4PX
-Foco: (p,0)
-Directriz: X=-p
-p>0 Abre a la derecha.
-p<0 Abre a la izquierda.
-Lado recto: 4.P
Eje de simetría "Y"
x2=4PX
-Foco: (0,p)
-Directriz: Y=-p
-p>0 Abre para arriba.
-p<0 Abre para abajo.
-Lado recto: 4.P
Eje de simetria "Y"
(x-h)2=4 p(y-k)
-Foco: (h,k+p)
-Directriz: y=k-p
-Longitud del lado recto: l 4p l
-Abre hacia abajo o hacia arriba.
Eje de simetría "X"
(y-k)2=4 p(x-h)
-Foco: (h,+p+k)
-Directriz: y=h-p
-Longitud del lado recto: l 4p l
-Abre a la derecha o la izquierda.
Ecuación Canónica V (h,k)

Eje focal "X"
-Focos: (-c,o) (c,o)
-vèrtices: (-a,o) (a,o)
-Punto de corte: (o,-b) (o,b)
Ejes Focales

Eje focal "Y"
-Focos: (o,-c) (o,c)
-Vértices: (o,-a) (o,a)
_Punto de Corte: (-b,o) (b,o)