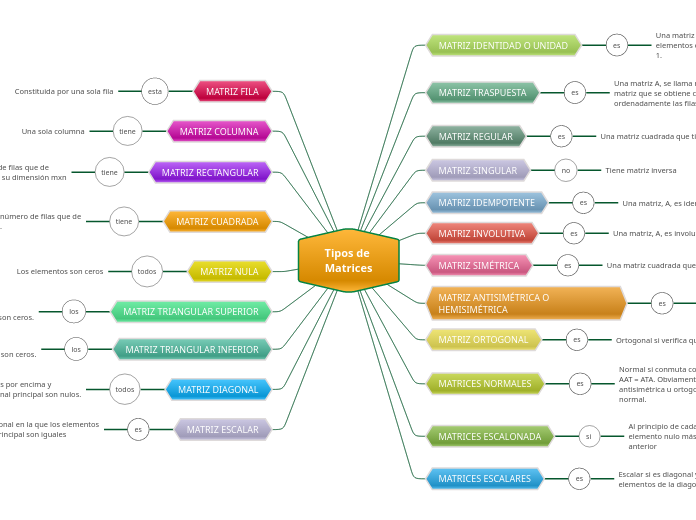
Tipos de Matrices
MATRIZ IDENTIDAD O UNIDAD
es
Una matriz diagonal en la que los
elementos de la diagonal principal son iguales a 1.
MATRIZ TRASPUESTA
es
Una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas
MATRIZ REGULAR
es
Una matriz cuadrada que tiene inversa.
MATRIZ SINGULAR
no
Tiene matriz inversa
MATRIZ IDEMPOTENTE
es
Una matriz, A, es idempotente si:
A elevado a la 2 = A.
MATRIZ INVOLUTIVA
es
Una matriz, A, es involutiva si:
A elevado a la 2 = I.
MATRIZ SIMÉTRICA
es
Una matriz cuadrada que verifica:
MATRIZ ANTISIMÉTRICA O HEMISIMÉTRICA
es
Una matriz cuadrada
que verifica:
A = -A elevado a la t.
MATRIZ ORTOGONAL
es
Ortogonal si verifica que:
A · A t= I.
MATRICES NORMALES
es
Normal si conmuta con su traspuesta, esto es, si AAT = ATA. Obviamente, si A es simétrica, antisimétrica u ortogonal, es necesariamente normal.
MATRICES ESCALONADA
si
Al principio de cada fila (o columna) un
elemento nulo más que en la fila (o columna) anterior
MATRICES ESCALARES
es
Escalar si es diagonal y además todos los elementos de la diagonal son iguales
MATRIZ FILA
esta
Constituida por una sola fila
MATRIZ COLUMNA
tiene
Una sola columna
MATRIZ RECTANGULAR
tiene
Distinto número de filas que de
columnas, siendo su dimensión mxn
MATRIZ CUADRADA
tiene
El mismo número de filas que de
columnas.
Los elementos de la forma aii constituyen la diagonal principal.
La diagonal secundaria la forman los elementos con i+j = n+1.
MATRIZ NULA
todos
Los elementos son ceros
MATRIZ TRIANGULAR SUPERIOR
los
Elementos situados por
debajo de la diagonal principal son ceros.
MATRIZ TRIANGULAR INFERIOR
los
Elementos situados por
encima de la diagonal principal son ceros.
MATRIZ DIAGONAL
todos
Los elementos situados por encima y
por debajo de la diagonal principal son nulos.
MATRIZ ESCALAR
es
Una matriz diagonal en la que los elementos
de la diagonal principal son iguales