VECTORS
Introduction to Vectors
6.8 Linear Combinations &
Spanning Sets
Linear Combination of Vectors
- Noncollinear vectors of u and v follow au+bv. in this case a b represent scalars of real numbers
- This vector will be a diagonal of a parallelogram that is formed by the vectors
- I,j and k span R3, this will be a linear combination of these three vectors
Spanning Sets
- Follwowing a set of vectors such as (i,j) it will form a spanning set for R2, since it is a linear combination of these two vectors
- Infinite number of sets
- Any pair of nonzero, noncollinear vectors will span R2
6.7 Operations with Algebraic
Vectors in R3
Representation
- Vectors in R3 are 3-dimentional and can be represnted by OP=(a,b,c) OR OP= ai, bj,ck
- They are also unit vectors along x-axis
i=(1,0,0)
j=(0,1,0)
k=(0,0,1)
Adding and Multiplying by a Scalar
- Adding in R3 is a very similar process to R2
- Adding two vectors is the same as adding their components
- When we multiply we use the scalar quantity to our respected vector and its components
Position Vectors & Magnitude in R3
- To determine the magnitude of OP we can use this formula to prove such where OP= (a,b,c).
- To find magnitudes of a new vector we can use this magnitude formula where uv will be equivalent to a position vector since directions and magnitudes allow them to be equal
6.1 Vectors
Definitions
SCALAR - A mathematical quantity that only contains magnitude
ex. age, volume, area, speed, and temperature
VECTORS - A mathematical quantity that requires both magnitude and direction
ex. velocity, and weight
Geometric Vectors
- Geometric vectors contain 2 points; tail the initial point (A), and our final point the head (B)
- The length of our particular vector will corespond to the magnitude
- The first diagram represents the vector while the second represents the magnitude, it is essential to familiarize yourself with these two images
Algebraic Vectors
- Algebraic vectors relate to a coordinate system with 2-3 points and are referenced from a 2D or 3D plane
ex. A(1,2) B(3,4) = (2,2)
Opposite Vectors
Vectors that are opposite from eachother have the same magnitude and are parallel, however, not the same direction
Equal Vectors
Vectors will be equivalent if they contain the same direction and same magnitude and are parallel
- They can also be coincident which translates their vector without changing size or direction
6.2 Vector Addition
Parallelogram Law
- To determine the sum of any two vectors a and b we can use the parallelogram law that forms these two vectors when added from tip to tail as a resultant vector of a+b
- The resultant is what ultimately forms the rest of the paralleogram from tail to tail
- We can also translate vectors a and b by the tail to the head of vector a, therefore, the resultant is placed from the tail of a to head of b
Difference of Two Vectors
- We can find the difference of two vectors a and b by adding the opposite vector of b to a
- A second way is to arange them from tail to tail, this way a-b vector aligns to be added to b in order to achieve a
6.3 Scaler Multiplication
of of a Vector
Multiplication by Scalar
- This demonstartes a number k (scalar) on the vector of a for example to result in a new vector or ka.
- K can affect the direction and magnitude of any vector when multiplied
Properties
- There are properties of scalar multiplication that help us assess vectors more clearly
Collinear Vectors
Collinear - when vectors are parallel and lie on the same straight line and can be translated
- In cases where k=0; the result will always be the zero vector
- In cases where k=-1; magnitude will remain but direction will change to an opposite
Unit Vectors
- When a vector has a magnitude of 1, we can determine the unit vector by taking the original vector and dividing it by its respective magnitude
6.4 Properties of Vectors
Properties
- Continually so, there are more properties of vectors that we can follow in computation to evalute expressions and simplify any numerical or algebraic expression where addition or scalar multiplication can be applied to vectors
- These rules are neccessary for linear combinations and meant for simplicity
6.6 Operations with Algebraic
Vectors in R2
Representation
- OP can represent this vector in R2 as OP=ai+bj
- The standard unit vectors such as i and j lie along the x and y axes at i=(1,0) and j=(0,1)
Adding and Multiplying by a Scalar
- Adding vectors in component form means to add x and y values accordingly
- When we multiply vectors by scalars we use both the x and y values by the scalar
- We can do this by multiplying a and b individually by m in this example
Position Vectors & Magnitudes in R2
- In this instance A(x1,y1) and B(x2,y2) are two points they form a vector where AB=(x2-x1,y2-y1)
- A simple way to find it related positon vector is by using the appropriate formula
- The directions and magnitudes are the same of the position vector, making them equivalent
6.5 Vectors in R2 and R3
Position Vector
- A position vector has its head at a point of A(a,0) and its tale will lie at the origin of B(0,0)
Vectors in R2
- The xy-plane is also know as R2 where x and y lie respectively across any real numbers
- Lie flat however, are infinitely far in any direction while they are 2-dimentional
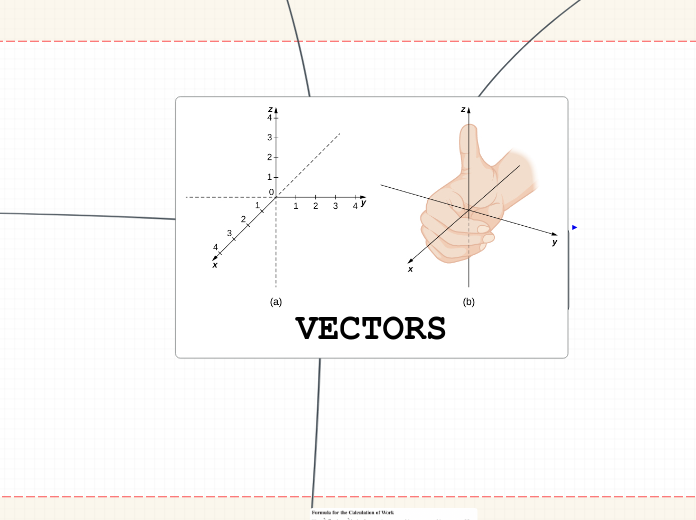
Vectors in R3
- Contains the xyz-plane that lie infinitely in positive and negative directions
- Runs along the x-axis and parallel to the y-axis and z axis
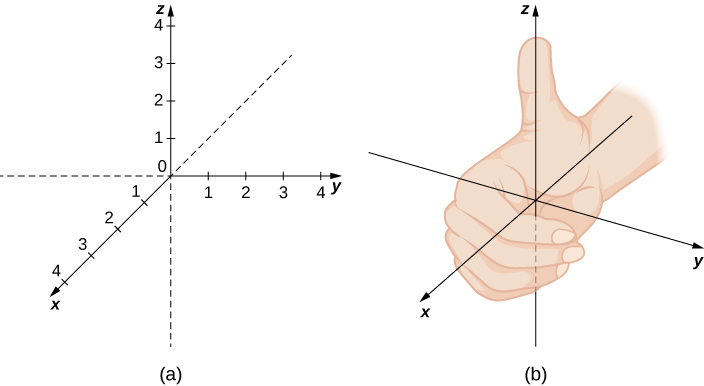
- R3 forms a right handed system where the three axes are perpendicular
Equations of Lines & Planes
8.1 Vector & Parametric
Equations in R2
Vector Equations of a Line
General Vector Equation
- Must be given either two distinct points or one point and a vector that defines the direction of the line.
- From this diagram we require a given point Po(x0,y0)
- As well as our direction point m=(a,b), where tm, tER will be any vector collinear with m.
Parametric Equation of a Line
- Vector form can be
modified to parametric form
- By expanding the right side, we equate x and y components into our new form
- In both vector or parametric forms, t can be given the name of a parameter
- Thus t can be replaced with any real number to obstain coordinate points
Parallel Lines
- To infer whether two lines are parallel from eachother L1 and L2 must have corresponding directional vectors of the same slopes
m1=m2
- Same directional vectors
m1=km2
- Directional vectors could be scalar multiples
m1xm2=0
- Cross product equals 0
Perpendicular Lines
- To determine whether two lines are perpendicular we must observe the following
m1 ⟂ m2
- If the two directional vectors are perpendicular
m1·m2 = 0
- If the dot product is equal to 0
8.2 Cartesian
Equation of a Line in R2
Cartesian Equation
Standard Form/
Cartesian Equation of a Line
n= (A,B) representing a normal line to this vector
A normal to this line is a vector that runs from the orgin perpendicular to a certain line to the point of N(A,B)
Parallel Lines
Lines L1 and L2 have normals n1 and n2
n1=kn2, kER, K≠0
- Parallel if and only their normals are scalar normals
- Lines of direction vectors will also be scalar multiples
Perpendicular Lines
n1·n2=0
- Perpendicular if and only dot product is zero
- Dot product of direction vectors will also be 0
Angle Between Normals
- Angles between 2 lines are defined by angles inbetween their directional vectors of a and b
8.3 Vector, Parametric
& Symmetric Equations
of a Line in R3
Vector Equation
- In this case our r0=(x0,y0,z0) where our vector is from the orgin to a point on a line
- Correspondingly, m=(a,b,c) will be a directional vector of a line
- To find a vector equation for a line in R3 it requires either two points or a point and a direction vector be given
Parametric Equation
- Our parametric equation will look a little different as well as it is now functioning in R3
Symmetrical Equation
- For the first time we are introduced to Symmetrical Equation of Lines in R3
- It is derived from a parametric equation and altered to provide you with the information you need while converting easily from one form to another, as all three forms depend on information
8.4 Vector & Parametric
Equations of a Plane
A Plane
- Planes are flat surfaces that extend in very distant directions indefinitely
- Also represented by the symbol π
A plan can be determined in 4 ways:
1. A line and a point not on a line
2. Three non collinear points
3. Two intersecting Lines
4. Two Parallel and non-coincident Lines
- When granted any of these four conditions, we can then form a plane and each will be unique to the other
Vector Equation of Plane
- In R3 a vector equation takes on an additional directional vector; where r0=(x0,y0,z0) is a point on the plane, while two noncollinear vectors of a=(a1,a2,a3) and b=(b1,b2,b3)are directional vectors
Observations:
- Always requires two directional vectors (s and t) since a plane is two-dimensional
-(S and t) generate all points on a plane since they are any real numbers
QUESTION & ANSWER
Parametric Equation
- A parametric equation of a plane is still achievable in R3
- However it is not possible to derive a symmetric equation of a plane
8.5 The Cartesian
Equation of a Plane
Cartesian Equation
- The normal is this case has to be a nonzero vector that is perpendicular to all other vectors in the plane
- There is only one line than can be drawn through an orgin that is perpendicular to the plane
- This line is better known as the normal axis.
- Thus to determine the equation of this Cartesian plane we can gather two points on a plane and a normal
Angles Between Two Intersecting Planes
- To determine angle 𝜃 between two planes of π1 and π2 with two normals, we can use the formula as follows
Parallel & Perpendicular Planes
Perpendicular if and only π1 and π2 are perpendicular planes and have normals that will also be perpendicular (n1·n2=0)
Parallel if and only π1 and π2 are parallel planes, then their normals will be parallel as well (n1=kn2) where k ≠ 0
Real Life Applications
Architecture
- Architecture is a key element and example of vectors in our every day life.
- Engineers especially structural and civil engineers deal with blueprints, forces, as well as magnitudes, and direction in their line of work
- This goes for anyone else involved in such activties that reqyure vectors
- Engineers specifically rely on stable structures to sustain and weight and enviromental factors.
- It is common for their work to include a lot of math and calculations of resultant forces in order to qualify and be approved for a safe space
Sports/Physical Exercise
- Sports and any common exercise are just a few examples of a great representation of vectors to apply in our real life.
- Vectors are used to calculate, practice and learn from when mastering skills and precision
- We can notice it the way we talk about players, or how far a a ball traveled
- Once more the force exerted when playing sports also grants a sense of direction and distance in a desired motion
- Force grants control and these things are highly monitored in the world of sports and calculated based on ranking of agility and force, amongt other factors
Applications of Vectors
7.1 Vectors as Forces
Equilibrium
Equilibriant - Keeps the object in a state of equilibrium as a single forces opposes the resultant of the force acting on the object
In the state of equilibrium the net effect of forces causes rest or a halt of zero movement
- Three non-collinear forces like that of a triangle must hold true to prove a,b≥c in order to maintain the equilibrium
- With collinear vectors the sides a,b,c need to lie along the same straight line
Resolving a Vector
- When a vector has both horizontal(i) and vertical(j) components we can take a single force and split it into two compounds. When resolved 𝜃 will be the angle that f makes with the x axis.
Force
- Force is a VECTOR
- Genrally speaking, it is something that can push or pull at which a motion changes or tends to its change or rest of motion
-Force is described by both magnitude and direction, thus resulting as a vector, the same rules apply to forces
- Forces undergo ACCELERTION on an object
- Just as the MAGNITUDE of a force is measured in newtons (N)
GRAVITY- a common example of a force that allows objects to accerlate at the rate of 9.8m/s2 approx.
Resultant & Composition of Forces
- When an object has two or more forces acting on it, a single force that represents the resultant force will combine the effects of all forces.
- The single force follows the same rule as adding two vectors
7.2 Velocity
Applications
Air Velocity
- When an object travels a resultant velocity is created simialrly to a change of direction in the object since it is relative to a person on the respective object
Ground Velocity
- When an object travels a resultant velocity is formed similarly to a change of direction in the object since it is realtive to a peroson on the ground with wind or an added current
Vector
Velocity- a vector quantity where both direction and magnitude play an essential role in determining the resultant velocity
- The resultant velocity of two vectors will always be its sum
- The velocity of an object will always be relative to its reference that influences its state
The resultant velocity
7.3 The Dot Product of Vectors
Properties
- All four of these properties help us further expand our knowledge and use of the dot product to determine and fufill certain requirements of questions
Dot Product
Dot Product
- The dot product is always scalar
- It represents the length that one vector can travel to the direction of another
- It is important to note that when two non-zero vectors are perpendicular, the dot product remains 0 always
- Works for both geometric and algebraic vectors
- VALUE of dot product is determined by angle between two vectors
Algebraic Vectors in R2 and R3
7.4 Scalar & Vector Projections
Scalar Projections
- Scalar Projections are the length of a vector projection (a number specifically)
- In this scalar projection a is dependent on the length of b
- If the angles between two vectors are between 0-90 degrees then the result is a positive scalar projection, anything between 90-180 degrees is negative. When it is equal to 90 degrees there is a projection of zero.
Vector Projections
- In a vector projection we take the scalar projection and multiply it by a unit vector in a direction onto which the other one will be projected
QUESTION & ANSWER
Directional Angles in R3
- Directional angles are angles in which a position vector makes with positive coordinate axes of x,y,z
- In order to find this, the projection of x,y,z of the direction vector must be placed onto each axis by the unit vector that acts correspondingly
7.5 Cross Product
Cross Product
- The cross product is denoted as axb
- It can also be referred to as the vector product since the result is a vector
- The cross product of two vectors will always be the vector that is perpendicular to them
- This unique observation also forms a RIGHT-HANDED system with two non-collinear vectors and its cross product
- We can use this formula to calculate the cross product of algebraic vectors
Properties
- There are 3 properties of the cross product
- It is important to keep in mind that in this case changing the order of multiplication does affect the result
7.6 Applications of
Dot & Cross Products
Applications of Dot Product
WORK- is a scalar quantity that measures in joules (J)
- It is when a force acts on an object so it moves from one point to another, therefore, it is the product of the distance of an object and the force along with it
Applications of Cross Product
TORQUE - is a vector quantity that is measured in newton meters or joules (J)
- A force is applied at point N and roated to point M
- The vector is perpendicular to the plane formed by its vectors r and f
Area of a Parallelogram
- Using the cross product, area of a parallelogram can be calculated by taking the magnitude between its base and height