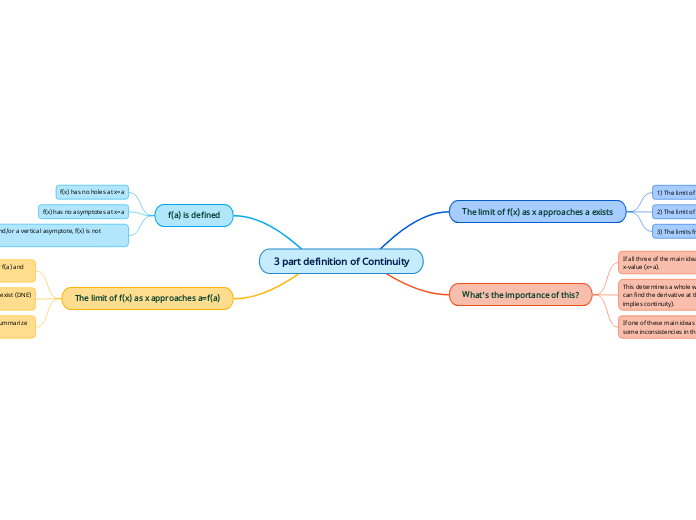
3 part definition of Continuity

The limit of f(x) as x approaches a exists

1) The limit of f(x) as x approaches a FROM THE LEFT exists.

2) The limit of f(x) as x approaches a FROM THE RIGHT exists.

3) The limits from the left and right equal each other.

What's the importance of this?

If all three of the main ideas are met, f(x) is continuous at this x-value (x=a).

This determines a whole world of things like for instance, if we can find the derivative at that certain x-value (differentiability implies continuity).

If one of these main ideas are not met, we know that there is some inconsistencies in the graph (discontinuities).

f(a) is defined

f(x) has no holes at x=a

f(x) has no asymptotes at x=a

If f(x) has a hole and/or a vertical asymptote, f(x) is not continuous at x=a

The limit of f(x) as x approaches a=f(a)

1) Although you might get two different numbers for f(a) and the limit, the numbers HAVE TO BE EQUAL

If you get that f(a) isn't defined or the limit does not exist (DNE) then this function isn't continuous at that x-value.

If they are equal and this theorem can be applied, summarize your work in a short explanation.