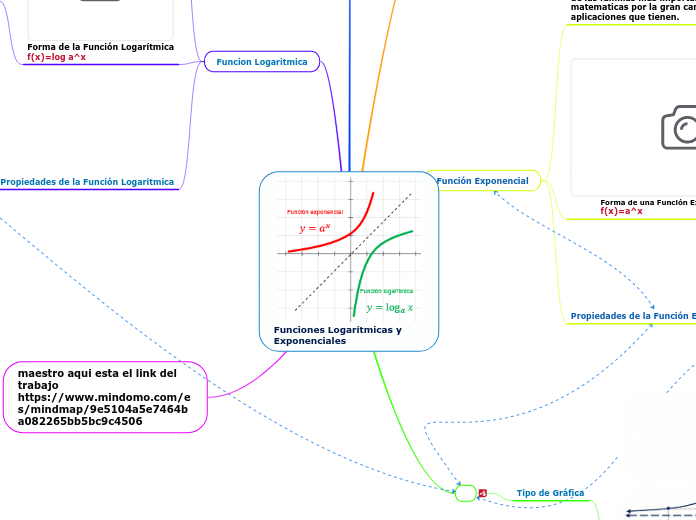
Funciones Logarítmicas y Exponenciales
¿Que es?
Las funciones exponenciales y = ax funciones logarítmicas logay = x se le denominan funciones transcendentales, ya que son funciones que transcienden el álgebra en el sentido que ninguna puede ser expresada en términos de una secuencia finita de operaciones algebraicas de suma, resta y/o extracción de raíces.

Función Exponencial
Las funciones exponenciales son una de las familias mas importantes en la matematicas por la gran cantidad de aplicaciones que tienen.
Definición

Forma de una Función Exponencial f(x)=a^x
Describe
Situaciones Complejas
Crecimiento Exponencial
Por Ejemplo



Decrecimiento exponencial
Propiedades de la Función Exponencial
1: Su dominio es R (conjunto de números reales)
2: Su rango es R+ (conjunto de números reales positivos)
3: Su gráfica es continua
4: Los puntos(0,1) y (1,a) siempre pertenecen a la gráfica
5: Es una función biyectiva
6: Es creciente si a >1
7: Es decreciente si a <1
8: Las curvas y=a^x , y=(1)^x
a son simetricas respecto del eje Y.
Tipo de Gráfica

Subtopic
TIPOS DE FUNCIONES LOGARITMICAS Y EXPONENCIALES
Funcion Logaritmica
Es aquella que generalmente se expresa como f(x)==logax siendo la base de esta funcion que ha de ser positiva y distinta de 1.
La funcion logaritmica es la inversa de la funcion exponenxial dado que: loga x=b<..> ab=x
Definición

Forma de la Función Logarítmica
f(x)=log a^x
Por Ejemplo

Para medir la magnitud de un terremoto

Propiedades de la Función Logarítmica
1:Su dominio es R+(conjunto de los números reales positivos)
2:Su rango es R(conjunto de los números reales)
3:Su gráfica es continua
4:Los puntos(1,0)y(a,1) siempre pertenecen a la gráfica
5:Es una función biyectiva
6:Es creciente si a>1
7:es decreciente si a<1
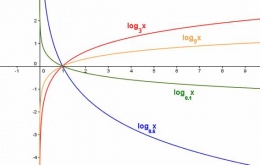
Tipo de Grafica