La idea de construir nuevas funciones a partir de funciones conocidas, hace pensar en
la pregunta: ¿Si se intercambian el dominio y el rango de una función f y por consiguiente
se intercambian los elementos de cada par ordenado de f, se obtiene una función? Se
observa que si un elemento y del rango de f es imagen de al menos dos elementos diferentes x1
y x2
del dominio, al efectuar el intercambio propuesto se tendría un elemento y
que poseería dos imágenes, lo cual contradice la definición de función.
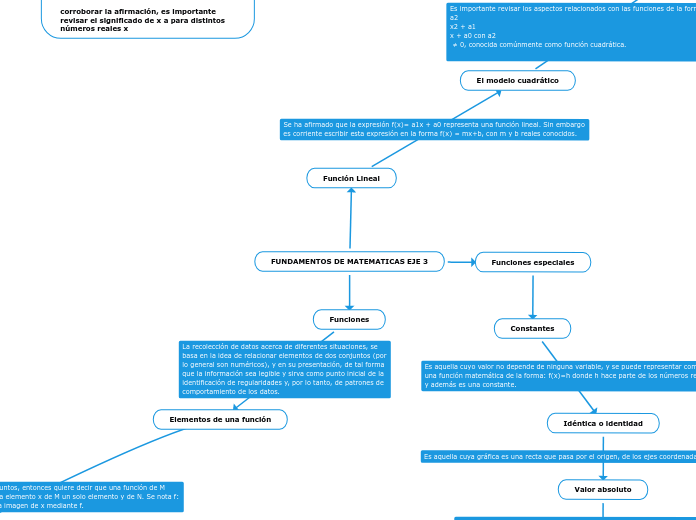
Es importante revisar los aspectos relacionados con las funciones de la forma f (x) =
a2
x2 + a1
x + a0 con a2
≠ 0, conocida comúnmente como función cuadrática.
Se ha afirmado que la expresión f(x)= a1x + a0 representa una función lineal. Sin embargo
es corriente escribir esta expresión en la forma f(x) = mx+b, con m y b reales conocidos.
Este tipo de funciones poseen un dominio definido por
varios intervalos y para cada uno de ellos, existe una regla
que permite encontrar el correspondiente contradominio. Se
debe tomar cada parte como una función independiente,
esto para lograr comprenderla con facilidad.
Es aquella que se simboliza como |x|, |x| transforma cualquier valor de x en su idéntico
Es aquella cuya gráfica es una recta que pasa por el origen, de los ejes coordenadas y su pendiente es m=1.
Es aquella cuyo valor no depende de ninguna variable, y se puede representar como
una función matemática de la forma: f(x)=h donde h hace parte de los números reales
y además es una constante.
Como se estableció anteriormente el dom f ⊂ X en tanto la ran f ⊂ Y se pueden establecer los elementos de la variable independiente que intervienen en la función y de acuerdo
a estos los valores que intervienen en la variable dependiente.
Por ejemplo el dominio y el rango de:
f (x) = raíz de x - 1
Por ser una raíz cuadrada la expresión x-1 debe ser mayor que cero entonces:
x -1 > 0 por tanto x >1
Es decir, toma los valores [1, ∞) para el dominio o valores de X, mientras para Y se tiene
que raíz de x -1 > 0 siempre es un valor positivo por tanto el recorrido o rango es [0, ∞).
Si M y N hace referencia a dos conjuntos, entonces quiere decir que una función de M
en N, es una regla que asigna a cada elemento x de M un solo elemento y de N. Se nota f:
M→ N. El elemento y se denomina la imagen de x mediante f.
La recolección de datos acerca de diferentes situaciones, se
basa en la idea de relacionar elementos de dos conjuntos (por
lo general son numéricos), y en su presentación, de tal forma
que la información sea legible y sirva como punto inicial de la
identificación de regularidades y, por lo tanto, de patrones de
comportamiento de los datos.