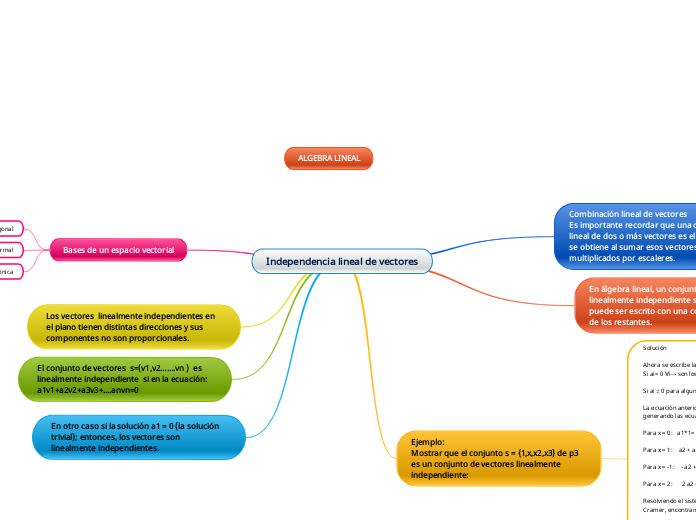
Independencia lineal de vectores
Combinación lineal de vectores
Es importante recordar que una combinación lineal de dos o más vectores es el vector que se obtiene al sumar esos vectores multiplicados por escaleres.
En álgebra lineal, un conjunto de vectores es linealmente independiente si ninguno de ellos puede ser escrito con una combinación lineal de los restantes.
Ejemplo:
Mostrar que el conjunto s = {1,x,x2,x3} de p3 es un conjunto de vectores linealmente independiente:
Solución
Ahora se escribe la ecuación a1*1+ a2 + x + a3*x2 + a4*x3 =0
Si ai= 0 ∀i→ son los linealmente independiente.
Si ai ≠ 0 para alguna i → son linealmente independiente.
La ecuación anterior debe ser válida para todas x∈R; así, generando las ecuaciones siguientes
Para x = 0: a1*1= 0 → a1 = 0
Para x = 1: a2 + a3 + a4 = 0
Para x = -1: - a2 + a3 – a4 = 0
Para x = 2: 2 a2 + 4 a3 + 8 a4 = 0
Resolviendo el sistema homogéneo anterior por la regla de Cramer, encontramos que:
Matriz |A|=|■(1&1&1@-1&1&-1@2&4&8)|=12≠0
→ Solución única: a1 = a2 = a3 = a4 = 0
Por lo tanto, los vectores 1, x, x2, x3 son linealmente independientes.
Bases de un espacio vectorial
Base ortogonal
Base ortonormal
base canónica