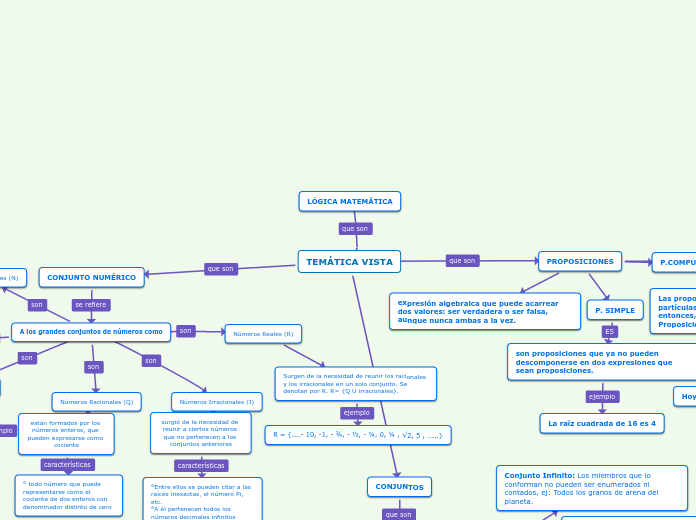
TEMÁTICA VISTA

CONJUNTO NUMÉRICO

A los grandes conjuntos de números como

Números fraccionario(Q+)

son aquellos que se expresan de las forma o como una expresión decimal periódica

Q+ = { 0, ½ , 2, 3/4 3, 9/7,.....}

°Dar solución a la división en el conjunto de los números naturales. °Cuando el dividendo es múltiplo del divisor y distinto de cero esta operación no tiene solución dicho conjunto.

Números Racionales (Q)

están formados por los números enteros, que pueden expresarse como cociente

° 5=5/1 ° 38= 38/1

° todo número que puede representarse como el cociente de dos enteros con denominador distinto de cero

Números Enteros (Z)

están formados por los números positivos, los números negativos y el cero.

Z={3,-73,0,15,-25}

°pues cuando el sustraendo es mayor que el minuendo, esta sustracción no tiene solución en los Conjuntos Naturales y Cardinales

Números Naturales (N)

surgió de la necesidad de contar, lo cual se manifiesta en el ser humano desde sus inicios.

° Tiene un número infinito de elementos °Cada elemento tiene un sucesor y todos, excepto el 1, un antecesor. °El sucesor de un número natural se obtiene sumando uno (+1); el antecesor se obtiene restando uno (-1)

N = { 1, 2, 3, 4, 5, 6, 7,.......}

Números Reales (R)

Surgen de la necesidad de reunir los racionales y los irracionales en un solo conjunto. Se denotan por R. R= {Q U irracionales}.

R = {....- 10, -1, - ¾, - ½, - ¼, 0, ¼ , √2, 5 , .....}

Números Irracionales (I)

surgió de la necesidad de reunir a ciertos números que no pertenecen a los conjuntos anteriores

°Entre ellos se pueden citar a las raíces inexactas, el número Pi, etc. °A él pertenecen todos los números decimales infinitos puros, es decir aquellos números que no pueden transformarse en una fracción.

PI=3,1415926535897932384626433832795

PROPOSICIONES

expresión algebraica que puede acarrear dos valores: ser verdadera o ser falsa, aunque nunca ambas a la vez.

P. SIMPLE

son proposiciones que ya no pueden descomponerse en dos expresiones que sean proposiciones.

La raíz cuadrada de 16 es 4

P.COMPUESTA

Las proposiciones en las que aparecen las partículas gramaticales como: No, o, y, si…entonces, si y solo si. Se les llama Proposiciones Compuestas o Moleculares.

Hoy es viernes y mañana es sábado.

TABLA DE VERDAD

es aquella que muestra el valor verdadero de una proposición compuesta, para cada combinación de verdad que se pueda asignar.

P v Q=FF=F. P ∧ Q=VV=V. P ⇒ Q=VF=F. P⇔ Q=VV y FF=V. P o Q=VV y FF=F

LÓGICA MATEMÁTICA

CONJUNTOS

Son una colección o agrupación que responden a una misma categoría.

Tipos de conjuntos

Conjunto Infinito: Los miembros que lo conforman no pueden ser enumerados ni contados, ej: Todos los granos de arena del planeta.

Conjunto Unitario: Están conformados por un solo elemento, ej: la letra A.

Conjunto Vacío: Carecen de elementos, son inexistentes , ej: un unicornio (ya que estos no existen).

Conjunto Referencial: Es un conjunto universal, en el entra tanto el conjunto A como el conjunto B, ej: A:"1,3,5..." B:"2,4,6..." UNIVERSAL: A Y B.

Conjuntos Equivalentes: Son aquellos conjuntos que poseen el mismo numero cardinal, la misma cantidad de elementos ej: A:"1,2,3,4,5" B:"a,b,c,d,e" contiene la misma cantidad.

Conjuntos Iguales: Esto se da cuando dos o mas conjuntos contienen iguales elementos, ej: A:"2,4,6,8" B:"8,6,4,2" ambos contienen los mismos elementos sin importar su orden.

Conjuntos Homogéneos: Los miembros o elementos que los componen responden al mismo genero o tipo, ej: A:"1,5,3,7,6,8" todos sus elementos son números.

Conjunto Heterogéneo: Compuesto por elementos que corresponden a distintos tipos, generos o clases, ej: el conjunto A contiene "2, J, perro, azul".