LOGICA MATEMÁTICA Y CONJUNTOS
Proposición : son oraciones que pueden ser verdaderas o falsas.
Hay dos pueden ser proposición simple (conformada por una sola oración) y compuesta (por dos o más proposiciones).

Conectivos lógicos: se usan para determinar la verdad de las proposiciones originales ( esto cuando una proposicion se construye apartir de otras proposiciones).
Subtema
Tablas de la verdad determina falso verdadero de las proposiciones.
Tautología: los valores son verdaderos.
Contradicción: los valores son falsos.
contingencia: los valores son falsos y verdaderos.
Teoría de conjuntos: Jorge Cantor.
Conjunto: colección de objetos
Se representan con letras mayúsculas y sus elementos se delimitan con llaves están separados por una coma.
Los conjuntos hay vacíos o nulos.
Subtema
Con ellos se construyen proposiciones matemáticas y explica conceptos como el de infinito.
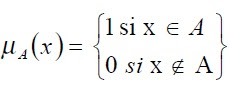
Pertenencia y no pertenencia.
Se definen de dos formas: enumeración (por medio de una lista de los elementos que la conforman) y compresión (regla de pertenencia).
Cardinalidad: numero de elementos que contiene un conjunto.
Finito: en ella la cardinalidad es definida.
Infinito: en ella la cardinalidad no esta definida.

Operaciones de conjuntos
Leyes del álgebra de conjuntos

Diagramas de VENN: en ella se presentan a los conjuntos y sus relaciones de manera sencilla e instructiva.
Razonamiendo inductivo
Se realiza mediante la observación de datos, reconocer patrones y hacer generalizaciones de dichos patrones.
Razonamiento analógico
Se realiza mediante premisas con las que se hace una analogía entre elementos
Razonamiento deductivo
Toma una premisa general y deduce conclusiones particulares.