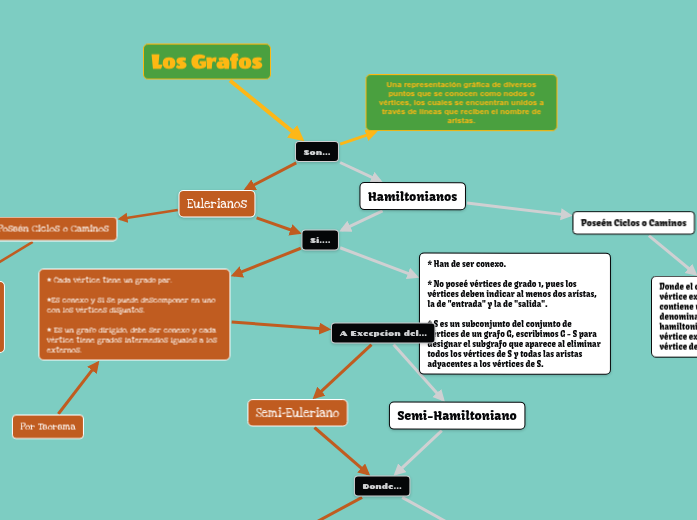
Los Grafos
Son...
Eulerianos
Si....
* Cada vértice tiene un grado par.
*Es conexo y si se puede descomponer en uno con los vértices disjuntos.
* Es un grafo dirigido, debe ser conexo y cada vértice tiene grados intermedios iguales a los externos.
* Han de ser conexo.
* No poseé vértices de grado 1, pues los vértices deben indicar al menos dos arístas, la de "entrada" y la de "salida".
* S es un subconjunto del conjunto de vértices de un grafo G, escribimos G − S para designar el subgrafo que aparece al eliminar todos los vértices de S y todas las aristas adyacentes a los vértices de S.
Poseén Ciclos o Caminos
A la cual el Caminio Euleriano recorre todas las aristas de un grafo una sola vez, pero que puede pasar por un mismo vértice varias veces. Cuando el camino comienza y termina en el mismo vértice se le denomina CICLO EULERIANO (circuito ó camino cerrado).
Ejemplo:

Hamiltonianos
Poseén Ciclos o Caminos
Donde el camino Hamiltoniano pasa por cada vértice exactamente una vez. Un grafo que contiene un camino hamiltoniano se denomina un ciclo hamiltoniano o circuito hamiltoniano si es un ciclo que pasa por cada vértice exactamente una vez (excepto el vértice del que parte y al cual llega).
Ejemplo:

Una representación gráfica de diversos puntos que se conocen como nodos o vértices, los cuales se encuentran unidos a través de líneas que reciben el nombre de aristas.
Por Teorema
A Execpcion del...
Semi-Euleriano
Semi-Hamiltoniano
Donde...
Poseé dos y solo dos Vertices
de grado impar.
No se cierra el ciclo, pero
atraviesa todos sus vértices.