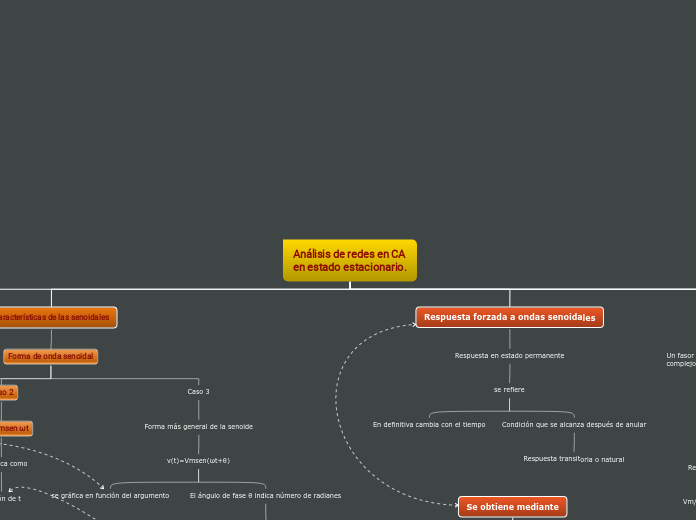
Análisis de redes en CA
en estado estacionario.
Respuesta completa de circuito eléctrico lineal
Respuesta natural
Respuesta forzada
Características de las senoidales
Forma de onda senoidal
Caso 1
v(t)= Vmsen ωt
Se gráfica como
función del argumento ωt
Se repite cada 2π radianes
Su periodo es consecuencia
Caso 2
v(t)= Vmsen ωt
Se gráfica como
función de t
Caso 3
Forma general de la senoide
v(t)=Vmsen(ωt+θ)
se gráfica en función del argumento
El ángulo de fase θ indica número de radianes
mediante los cuales la onda senoidal
se recorre hacia la izquierda o al tiempo anterior
Retraso
sen ωt
con respecto
sen (ωt+θ) en θ rad
Adelanto
de sen (ωt+θ)
por
−θ rad
θ rad.
Respuesta forzada a ondas senoidales
Respuesta en estado permanente
se refiere
En definitiva cambia con el tiempo
Condición que se alcanza después de anular
Respuesta transitoria o natural
Fasor
Un fasor es una representación gráfica de un número complejo
se expresa en la forma polar
Y=A/_φ
Resistencia
Vm/_θ=RImφ
Inductor
V=jωLI
Capacitor
I=jωCV
Impedancia
Medida de oposición que presenta
un circuito cuando se aplica tensión
Resistencia
Z=R
Capacitor
Z=1/jωC
Inductor
Z=jωL
Admitancia
Relación de
Corriente a Tensión
Parte Real
Conductancia
G
Parte Imaginaria
Susceptancia
B
Respuesta transitoria de corta vida
se presenta ante
Cambio repentino
Respuesta de estado permanente a largo plazo
Se presenta ante
Cualquier fuente independiente
El periodo es ahora T
su frecuencia es
1/T periodos cada segundo
Hertz Hz
ωT=2π
La onda senoidal debe acompletar
Obtenemos la relación entre la frecuencia y la frecuencia radial
ω=2πf
Se obtiene mediante
it=((RVm/(R^(2))+(ω^(2))(L^(2)))cosωt+(ωLVm)/(R^(2))+(ω^(2))(L^(2))sen ωt
Y=G+jB=1/Z=1/R+jX
Leyes De Kirchoff
Igualdades basadas
Conservación de la energía
Carga de los circuitos eléctricos
En el dominio del tiempo tenemos
v1t+v2t+···+vNt=0
sustituyendo la tensión real, por tensión compleja obtenemos
V1+V2+···+VN=0
Considerando un circuito RL
VR+VL=Vs
utilizando las relaciones V-I
RI+jωLI=Vs
La corriente fasorial en términos de la tensión de la fuente Vs:
I=Vs/R+jωL
Eligiendo una amplitud tensión de la fuente de Vm y un ángulo de fase de 0°
I= Vm/_0◦/R+jωL
La corriente puede transformarse al dominio de tiempo si se le escribe primero en la forma polar:
I=(Vm/√R2+ω2L2)[1−tan−1(ωL/R)]