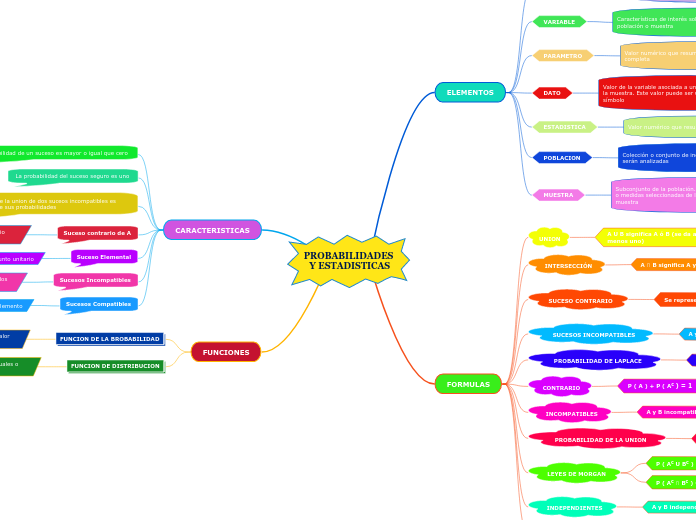
PROBABILIDADES Y ESTADISTICAS
ELEMENTOS
EXPERIMENTO
Actividad planeada cuyos resultados producen un conjunto de datos
VARIABLE
Características de interés sobre cada elemento de una población o muestra
PARAMETRO
Valor numérico que resume todos los datos de una población completa
DATO
Valor de la variable asociada a un elemento de la población o la muestra. Este valor puede ser un numero, una palabra o un símbolo
ESTADISTICA
Valor numérico que resume los datos de la muestra
POBLACION
Colección o conjunto de individuos, objetos cuyas propiedades serán analizadas
MUESTRA
Subconjunto de la población. Consta de los individuos, objetos o medidas seleccionadas de la población por el recolector de la muestra
FORMULAS
UNION
A U B significa A ó B (se da alguno de ellos, se da al menos uno)
INTERSECCIÓN
A ∩ B significa A y B (se dan ambos simultáneamente)
SUCESO CONTRARIO
Se representa AC , o bien Ā y se cumple:
A U Ac = E
A ∩ Ac = Ø
SUCESOS INCOMPATIBLES
A y B incompatibles cuando A ∩ B = Ø
PROBABILIDAD DE LAPLACE
Casos Favorables / Casos Posibles
CONTRARIO
P ( A ) + P ( Ac ) = 1
INCOMPATIBLES
A y B incompatibles
P ( A ∩ B ) = 0
PROBABILIDAD DE LA UNION
P ( A U B ) = P ( A ) + P ( B ) - P ( A ∩ B )
LEYES DE MORGAN
P ( Ac U Bc ) = P ( A ∩ B )c
P ( Ac ∩ Bc ) = P ( A U B )c
INDEPENDIENTES
A y B independientes
P ( A ∩ B ) = P ( A ) . P ( B )
CONDICIONADA
P ( A / B ) = P ( A ∩ B ) / P ( B )
CARACTERISTICAS
La probabilidad de un suceso es mayor o igual que cero
La probabilidad del suceso seguro es uno
La probabilidad de la union de dos suceos incompatibles es igual a la suma de sus probabilidades
Suceso contrario de A
Es el que ocurre cuando no se da A: es un complementario respecto al espacio muestral (A)
Suceso Elemental
Es el que tiene un solo resultado, es un conjunto unitario
Sucesos Incompatibles
La intersección es conjunto vacío, es decir, no pueden los dos sucesos darse al mismo tiempo
Sucesos Compatibles
La intersección de dos sucesos contiene algún elemento
FUNCIONES
FUNCION DE LA BROBABILIDAD
Es la probabilidad de que la variable aleatoria tome un valor particular
f ( xi ) = p ( X = x )
FUNCION DE DISTRIBUCION
Es la probabilidad de que la variable tome valores iguales o inferiores a x
F ( x ) = p ( X < x )