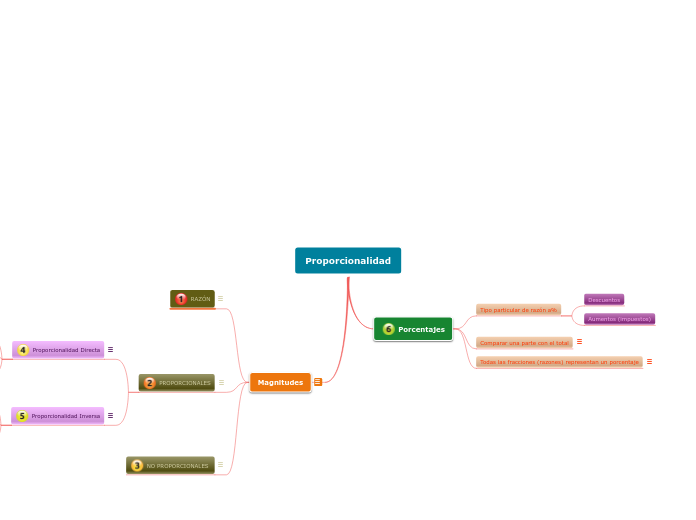
Proporcionalidad
Porcentajes
Tipo particular de razón a%
Descuentos
Aumentos (impuestos)
Comparar una parte con el total
Todas las fracciones (razones) representan un porcentaje
Magnitudes
RAZÓN
PROPORCIONALES
Proporcionalidad Directa
Cosntante de proporcionalidad
Propiedad entre razones
Reducir a la unidad
Proporcionalidad Inversa
Constante de proporcionalidad
Propiedad de la proporción
Reducir a la unidad
NO PROPORCIONALES