¿Qué tanto sabemos acerca de conjuntos?
¿Cómo se representan?
Es habitual representar los conjuntos en forma gráfica mediante los Diagramas de Venn .
En estos diagramas el conjunto se representa mediante una superficie limitada por una línea. En su interior se colocan los elementos del conjunto. Cada porción del plano limitada se nombra con una letra mayúscula.
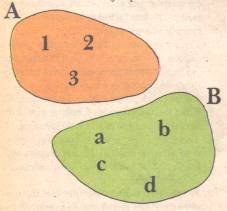
Ejemplo: El conjunto A está formado por los elementos 1, 2, 3.
El conjunto B está formado por los elementos a, b, c, d.
Existe, además, otra forma de representarlos que es entre llaves.
¿Qué son los conjuntos?
Un conjunto es la agrupación de diferentes elementos que comparten entre sí características y propiedades semejantes. Estos elementos pueden ser sujetos u objetos, tales como números, canciones, meses, personas, etc.
Clasificación
Finito: Sus elementos pueden contarse o enumerarse en su totalidad. Por ejemplo: los meses del año, los días de la semana o los continentes.
Infinito: Sus elementos no se pueden contar o enumerar en su totalidad, debido a que no tienen fin. Por ejemplo: los números
Conjunto unitario: Está compuesto por un único elemento. Por ejemplo: La Luna es el único elemento en el conjunto “satélites naturales de la Tierra”.
Conjunto vacío: No presenta ni contiene elementos
Notación de conjuntos
Por extensión: consiste en dar a conocer todos los elementos del conjunto, cada uno
Ejemplo: A = {a, e, i, o, u} es un conjunto en el que se indican todos sus elementos, por lo tanto se trata de un conjunto por extensión.
Por comprensión: Consiste en aquellos que sus elementos se indican de manera general sin indicar cada uno de ellos.
Ejemplo: {números pares menores o iguales a 10} no se indican todos sus elementos sino una regla general que los define, por lo tanto, es un conjunto por comprensión.
Operaciones básicas entre conjuntos
Unión: Es la operación que nos permite unir dos o más conjuntos para formar otro conjunto que contendrá a todos los elementos que queremos unir pero sin que se repitan.
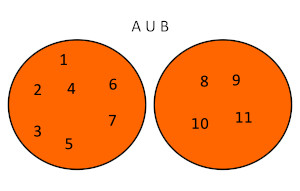
Ejemplo: Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la unión de estos conjuntos será A∪B={1,2,3,4,5,6,7,8,9}. Usando diagramas de Venn se tendría lo siguiente:
Intercepción: Es la operación que nos permite formar un conjunto, sólo con los elementos comunes involucrados en la operación. Es decir dados dos conjuntos A y B, la de intersección de los conjuntos A y B, estará formado por los elementos de A y los elementos de B que sean comunes, los elementos no comunes A y B, será excluidos
Ejemplo: Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la intersección de estos conjuntos será A∩B={4,5}. Usando diagramas de Venn se tendría lo siguiente:
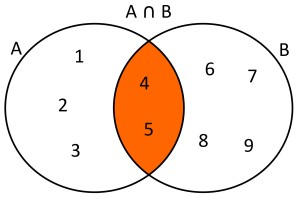
Diferencia simétrica: Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que tendrá todos los elementos que no sean comunes a ambos conjuntos. Es decir, dados dos conjuntos A y B, la diferencia simétrica estará formado por todos los elementos no comunes a los conjuntos A y B.
Ejemplo: Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia simétrica de estos conjuntos será A △ B={1,2,3,6,7,8,9}. Usando diagramas de Venn se tendría lo siguiente:
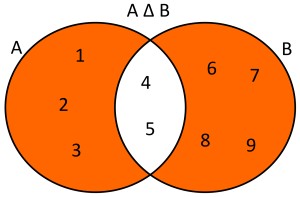
Diferencia de conjunto: Es la operación que nos permite formar un conjunto, en donde de dos conjuntos el conjunto resultante es el que tendrá todos los elementos que pertenecen al primero pero no al segundo. Es decir, dados dos conjuntos A y B, la diferencia de los conjuntos entra A y B, estará formado por todos los elementos de A que no pertenezcan a B
Ejemplo: Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la diferencia de estos conjuntos será B-A={6,7,8,9}. Usando diagramas de Venn se tendría lo siguiente:
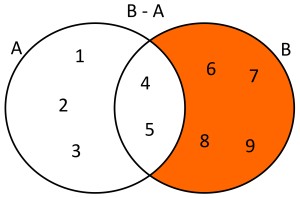
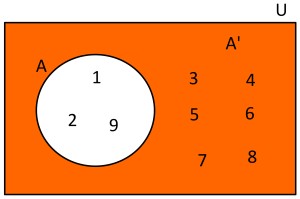
Complemento de un conjunto: Es la operación que nos permite formar un conjunto con todos los elementos del conjunto de referencia o universal, que no están en el conjunto. Es decir, dado un conjunto A que está incluido en el conjunto universal U, entonces el conjunto complemento de A es el conjunto formado por todos los elementos del conjunto universal, pero sin considerar a los elementos que pertenezcan al conjunto A.
Ejemplo: Dado el conjunto Universal U={1,2,3,4,5,6,7,8,9} y el conjunto A={1,2,9}, el conjunto A' estará formado por los siguientes elementos A'={3,4,5,6,7,8}. Usando diagramas de Venn se tendría lo siguiente: