Sistemas Lineares
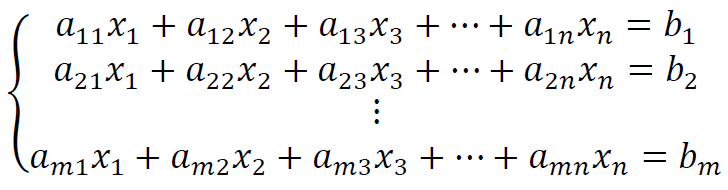
Definição
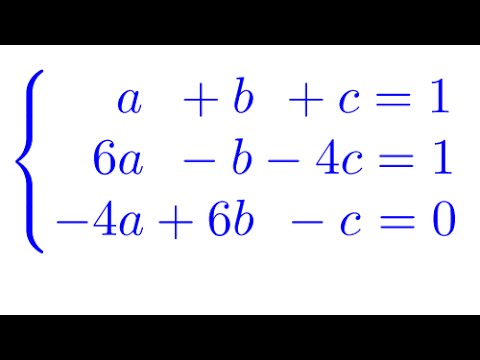
Exemplo
EQUAÇÃO LINEAR
Matemática
Tipos de sistema
POSSÍVEL

Determinado (SPD)
Indeterminado (SPI)
IMPOSSÍVEL (SI)
Métodos de Resolução
Escalonamento

Escalonamento por matriz
Escalonamento por sistemas
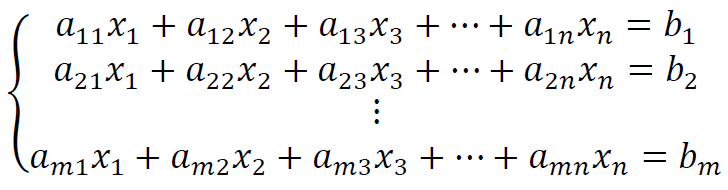
Um sistema linear é um conjunto de equações lineares, com m equações e n incógnitas.
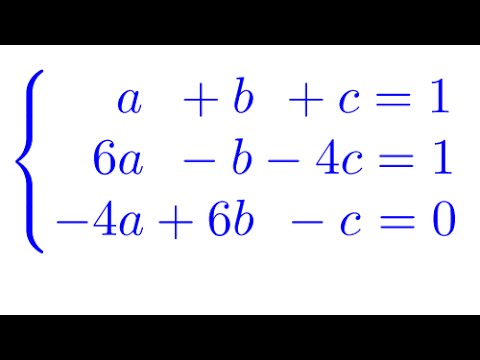
Exemplo
POSSÍVEL

Determinado (SPD)
Admite uma única solução, pois as retas são concorrentes, logo possuem um único ponto em comum.

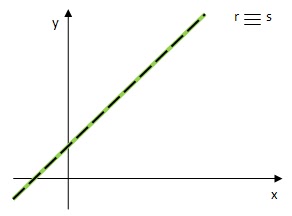
Indeterminado (SPI)
Admite infinitas soluções, pois as retas são paralelas coincidentes, logo possuem todos os pontos em comum.

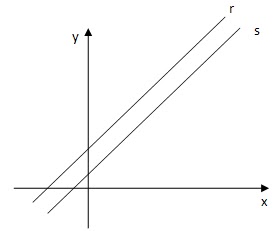
IMPOSSÍVEL (SI)
Não admite solução, pois as retas que compõem esse sistema são paralelas distintas, portanto não possuem pontos em comum.

Escalonamento por matriz
É possível transformar um sistema de equações lineares em uma representação matricial, e efetuar o escalonamento da matriz. Os coeficientes das incógnitas serão os elementos da matriz que ocuparão as linhas e as colunas de acordo com o posicionamento dos termos no sistema. Para encontrar essa representação matricial devemos realizar o seguinte procedimento:Os coeficientes da primeira equação ocuparão a primeira linha da matriz.As colunas deverão ser referentes à uma mesma incógnita.
Escalonamento por sistemas