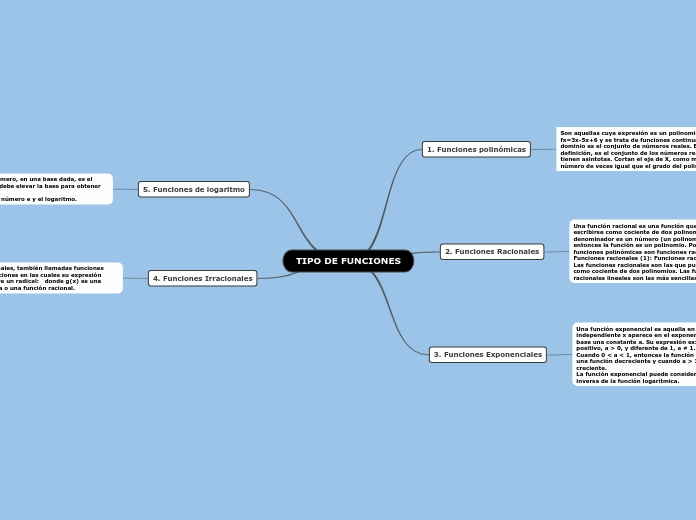
TIPO DE FUNCIONES
Funciones polinómicas
Son aquellas cuya expresión es un polinomio, ejemplo: fx=3x-5x+6 y se trata de funciones continuas, cuyo dominio es el conjunto de números reales. El dominio de definición, es el conjunto de los números reales. No tienen asintotas. Cortan el eje de X, como máximo, un número de veces igual que el grado del polinomio.
EJEMPLO: F(X)= mx + n
Funciones Racionales
Una función racional es una función que puede escribirse como cociente de dos polinomios. Si el denominador es un número (un polinomio de grado 0), entonces la función es un polinomio. Por lo tanto, las funciones polinómicas son funciones racionales. Funciones racionales (1): Funciones racionales lineales
Las funciones racionales son las que pueden escribirse como cociente de dos polinomios. Las funciones racionales lineales son las más sencillas de este tipo.
EJEMPLO: f(x)=P(x)/Q(x)
Funciones Exponenciales
Una función exponencial es aquella en que la variable independiente x aparece en el exponente y tiene de base una constante a. Su expresión es: Siendo a un real positivo, a > 0, y diferente de 1, a ≠ 1.
Cuando 0 < a < 1, entonces la función exponencial es una función decreciente y cuando a > 1, es una función creciente.
La función exponencial puede considerarse como la inversa de la función logarítmica.
EJEMPLO: a° =1
Funciones de logaritmo
El logaritmo de un número, en una base dada, es el exponente al cual se debe elevar la base para obtener dicho número.
Siendo a la base, x el número e y el logaritmo.
Funciones Irracionales
Funciones irracionales, también llamadas funciones radicales, son funciones en las cuales su expresión matemática incluye un radical: donde g(x) es una función polinómica o una función racional.