par Настя Демидова Il y a 3 années
772
уравнения
par Настя Демидова Il y a 3 années
772

Plus de détails
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
1.D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
2.D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
3.D < 0. Если дискриминант меньше нуля, тогда у квадратного уравнения нет корней.
В зависимости от полученных корней и знака коэффициента a, возможно одно из шести расположений графика функции у = ax2 + bx + c.
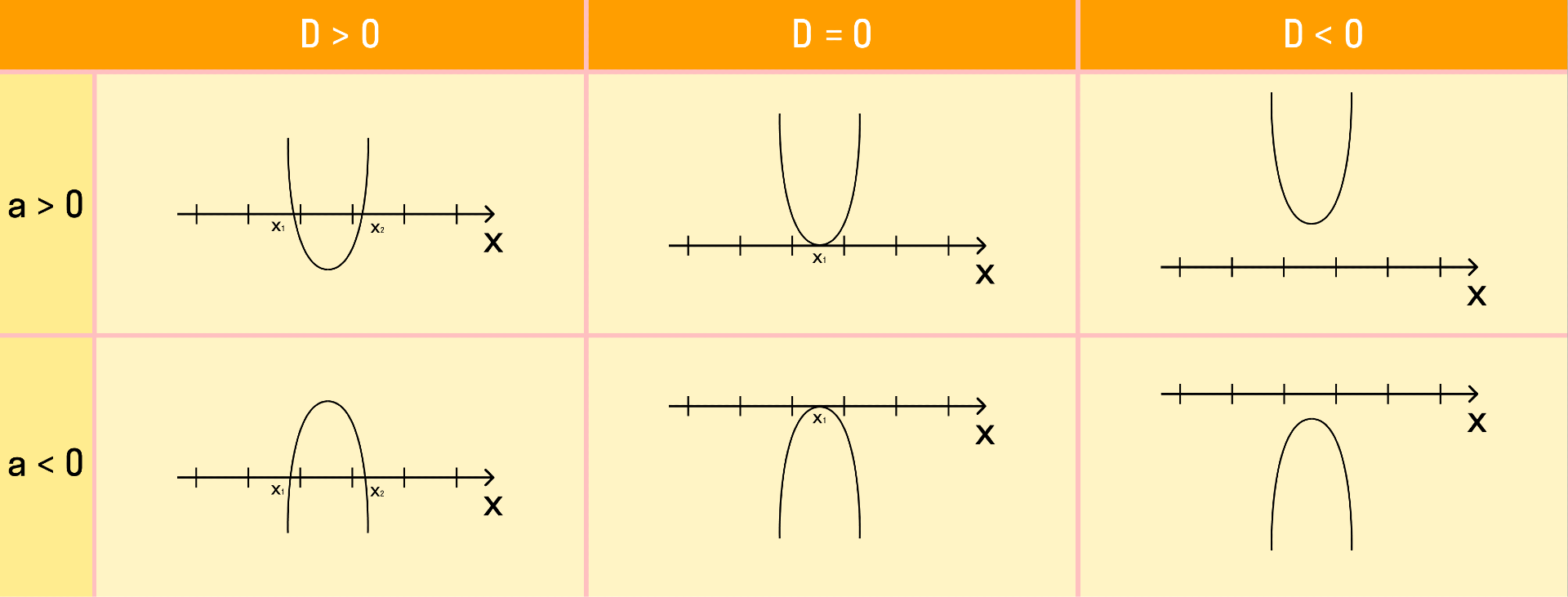
Если требуется найти числовой промежуток, на котором квадратный трехчлен ax2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если нужно найти числовой промежуток, на котором квадратный трехчлен ax2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
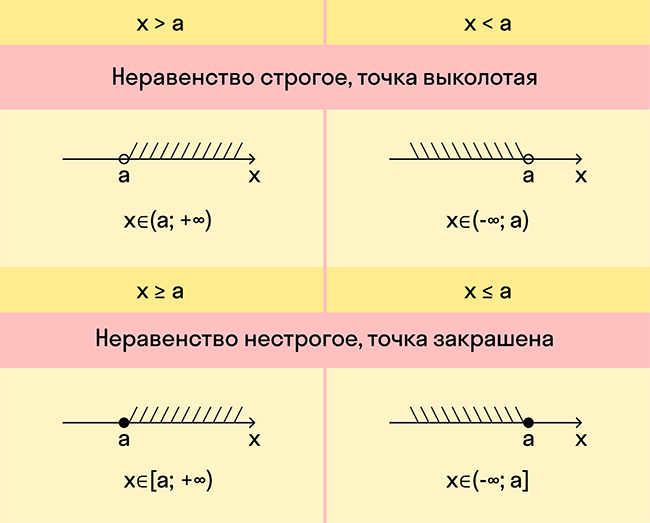
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.
Алгоритм решения квадратных неравенств методом интервалов:
1.Найти нули квадратного трехчлена ax2 + bx + c из левой части квадратного неравенства.
2.Изобразить координатную прямую и при наличии корней отметить их на ней.
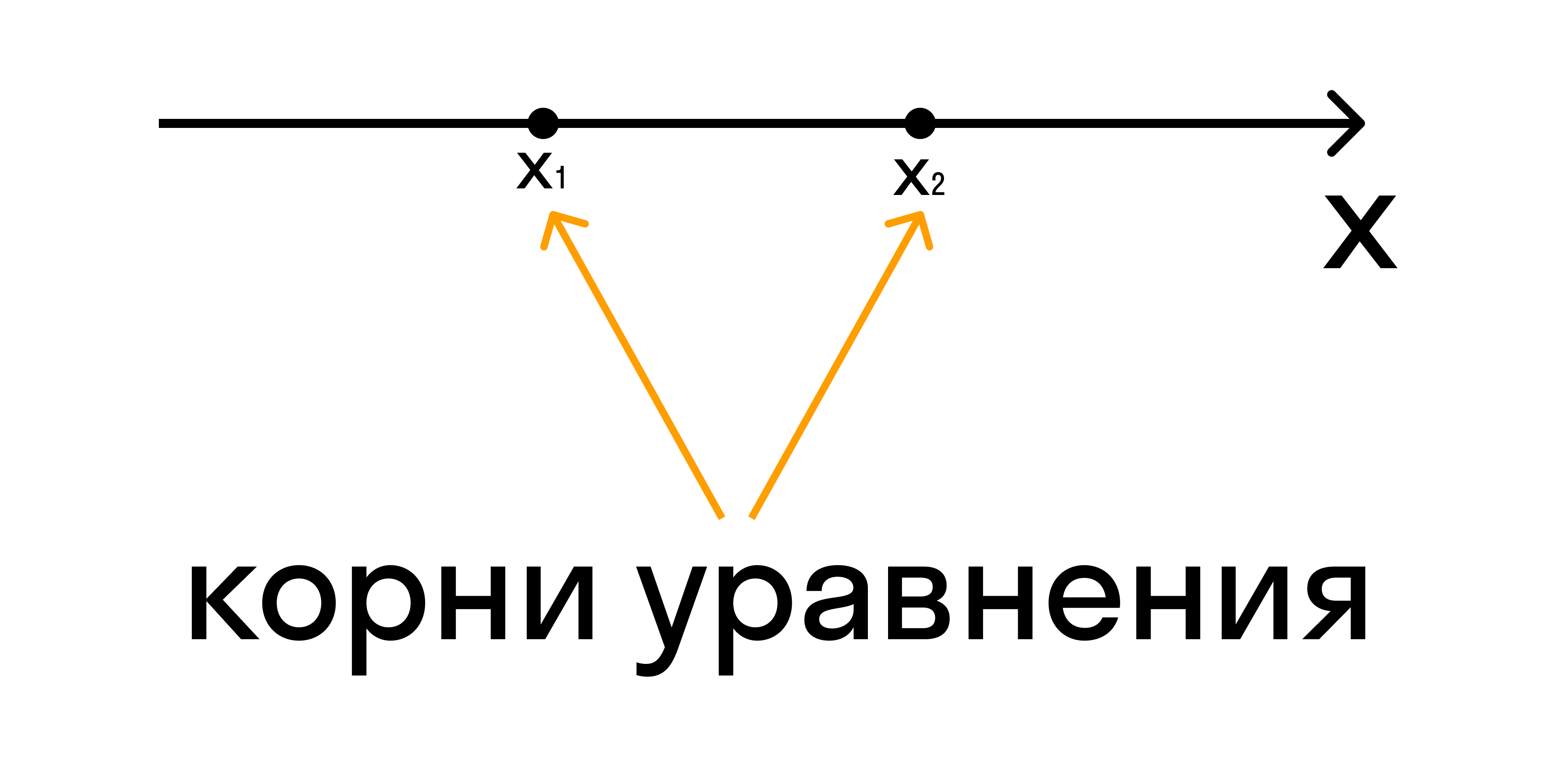
Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.
3.Определить, какие знаки имеют значения трехчлена на каждом промежутке (если на первом шаге нашли нули) или на всей числовой прямой (если нулей нет). И проставить над этими промежутками + или − в соответствии с определенными знаками. Источник -
4.Если квадратное неравенство со знаком > или ≥ — наносим штриховку над промежутками со знаками +.
Если неравенство со знаком < или ≤, то наносим штриховку над промежутками со знаком −.
В результате получаем геометрический образ некоторого числового множества — это и есть решение неравенства.
Либо вместо штриховки можно нарисовать «арки» для интервалов. Справа налево, начиная с +, проставить чередуя знаки + и −.
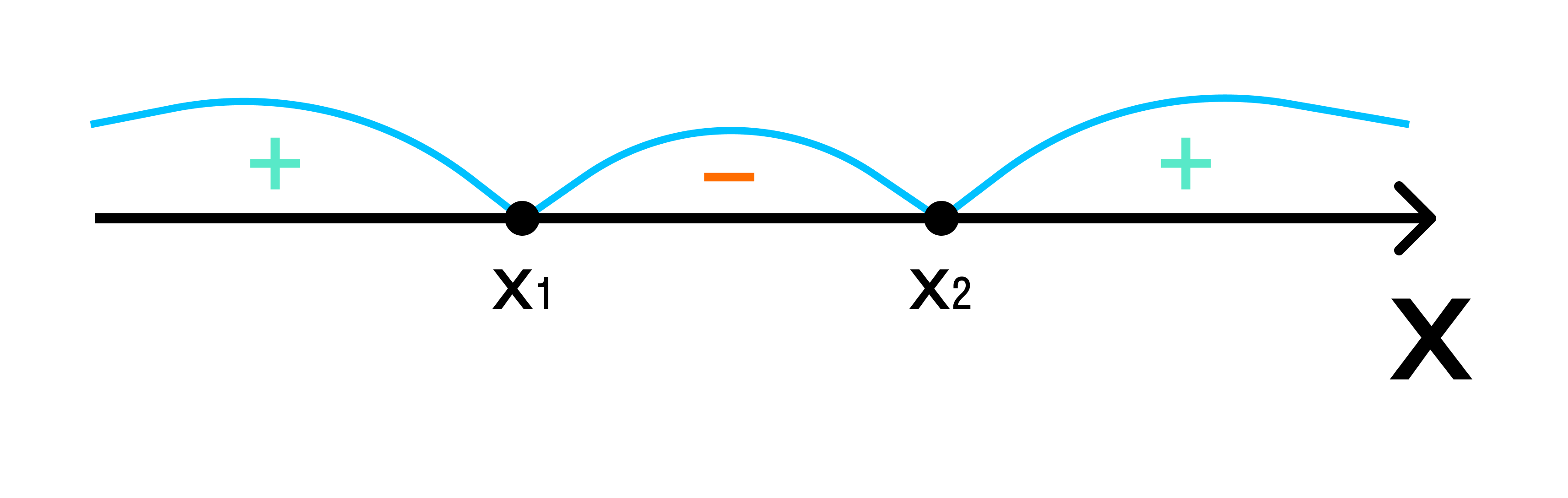
5.Выбрать необходимые интервалы и записать ответ.
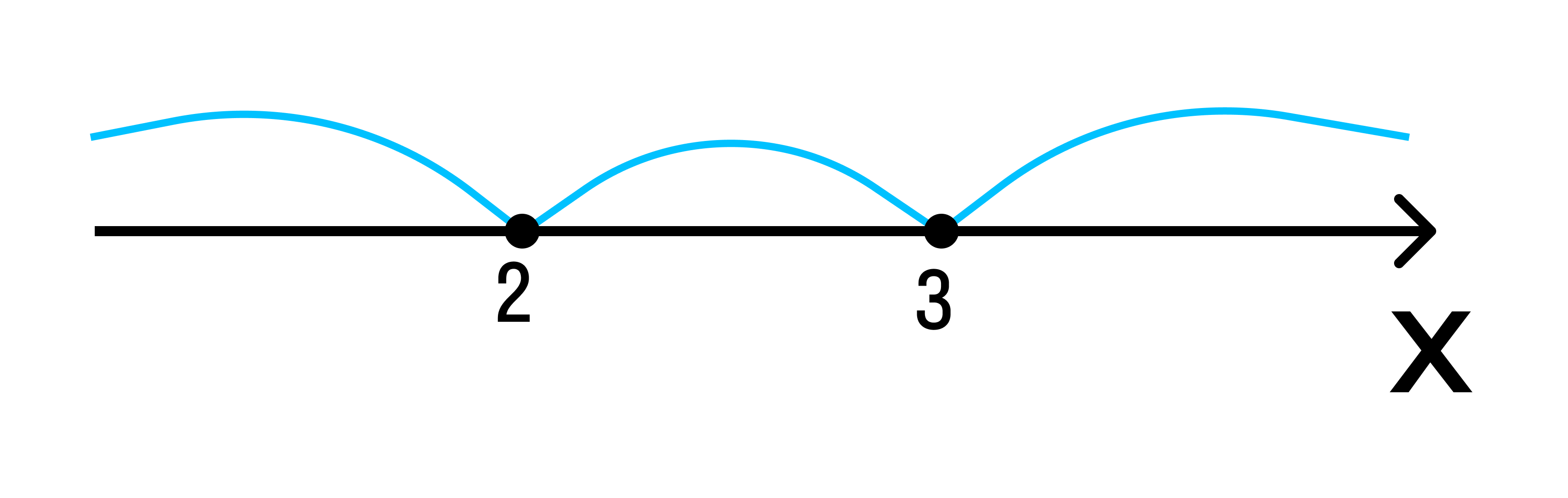
Пример 1. Решить неравенство методом интервалов: x^2 - 5x + 6 ≥ 0.
Как решаем:
Приравняем квадратный трехчлен к 0 и найдем нули:
x2 - 5x + 6 = 0
(x - 3) (x -2) = 0
x - 3 = 0
x - 2 = 0
x = 3
x = 2
Отметим полученные значения на числовой прямой:
Система неравенств с одной переменной – совокупность нескольких неравенств с одной и той же переменной. Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы. Решить систему неравенств – значит найти все ее решения или доказать, что решений нет.
Алгоритм решения систем неравенств:
1. Решить каждое неравенство системы.
2. Изобразить графически решения каждого неравенства на координатной прямой.
3. Найти пересечение решений неравенств на координатной прямой.
4. Записать ответ в виде числового промежутка.
Система, не имеющая решений, называется несовместимой.
Системы вида: ax-b<0 и cx+d<0 называются системами линейных неравенств с одной переменной. Вместо знака меньше могут быть и другие знаки сравнения.
Например: 
Изобразив на одной координатной прямой оба точечных множества, составляющих последнюю систему, получаем ответ примера:

Ответ: 
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
1.D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
2.D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
3.D < 0. Если дискриминант меньше нуля, тогда у квадратного уравнения нет корней.
В зависимости от полученных корней и знака коэффициента a, возможно одно из шести расположений графика функции у = ax2 + bx + c.

Если требуется найти числовой промежуток, на котором квадратный трехчлен ax2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если нужно найти числовой промежуток, на котором квадратный трехчлен ax2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.
Пример 1. Решить неравенство методом интервалов: x^2 - 5x + 6 ≥ 0.
Как решаем:
1.Приравняем квадратный трехчлен к 0 и найдем нули:
x2 - 5x + 6 = 0
(x - 3) (x -2) = 0
x - 3 = 0
x - 2 = 0
x = 3
x = 2
2.Отметим полученные значения на числовой прямой:

3.Расставим знаки на полученных промежутках:
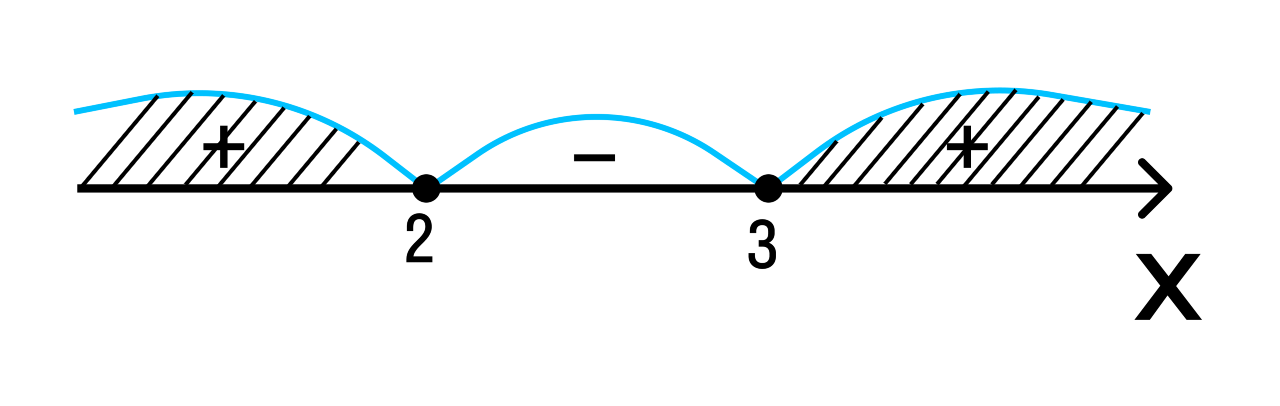
Ответ: х ≤ 2, х ≥ 3.
Подробнее материал можно изучить здесь: https://skysmart.ru/articles/mathematic/metod-intervalov-reshenie-neravenstv
Рациональным называется неравенство, в левой и правой частях которого — рациональные выражения.
Рассмотрим один из методов решения рациональных неравенств — метод интервалов. Этот метод основан на использовании графика функции.
Рассмотрим один из методов решения рациональных неравенств — метод интервалов. Этот метод основан на использовании графика функции.
Предположим, что нужно решить неравенство 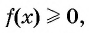 где
где 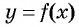 — функция, график которой изображен на рисунке 80. Тогда для решения неравенства
— функция, график которой изображен на рисунке 80. Тогда для решения неравенства 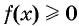 достаточно указать значения аргумента, при которых значения функции
достаточно указать значения аргумента, при которых значения функции 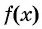 неотрицательны, т. е. при которых график функции лежит не ниже оси абсцисс. Это промежутки [-6; -2] и [2; 8]. Следовательно, все решения неравенства
неотрицательны, т. е. при которых график функции лежит не ниже оси абсцисс. Это промежутки [-6; -2] и [2; 8]. Следовательно, все решения неравенства 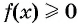 — это все значения переменной
— это все значения переменной 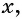 принадлежащие объединению множеств
принадлежащие объединению множеств 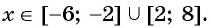
Заметим, что такие же решения имеет неравенство 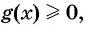 — функция, график которой изображен на рисунке 81, так как значения функции
— функция, график которой изображен на рисунке 81, так как значения функции 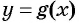 неотрицательны при тех же значениях переменной, что у функции
неотрицательны при тех же значениях переменной, что у функции 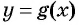 .
.
Таким образом, для применения метода интервалов к решению неравенства достаточно построить схему графика функции, на которой отражены только некоторые (необходимые для решения неравенства) свойства функции, а именно ее область определения, нули и промежутки знакопостоянства.

Решите неравенство
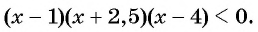
Решение:
Рассмотрим функцию 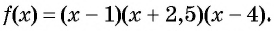 Построим схему графика этой функции, по которой определим ее промежутки знакопостоянства. Для этого найдем точки пересечения графика с осью абсцисс, т. е. нули этой функции:
Построим схему графика этой функции, по которой определим ее промежутки знакопостоянства. Для этого найдем точки пересечения графика с осью абсцисс, т. е. нули этой функции: 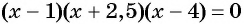 при
при 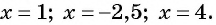
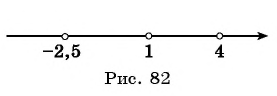
Отметим нули функции на оси абсцисс (рис. 82). Так как данное неравенство строгое, то нули функции отметим на оси пустыми точками.
Нули функции разбили ось на четыре промежутка. Определим, выше или ниже оси абсцисс расположен график функции в каждом из полученных промежутков.
Поскольку правее точки 4 каждый из трех множителей произведения 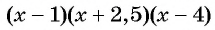 принимает положительные значения, то при
принимает положительные значения, то при 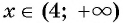 график функции
график функции 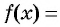
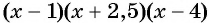 расположен выше оси абсцисс.
расположен выше оси абсцисс.
При переходе через каждую из отмеченных точек знак функции 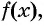 а значит, и положение графика относительно оси абсцисс меняется, так как меняется знак одного из множителей.
а значит, и положение графика относительно оси абсцисс меняется, так как меняется знак одного из множителей.
Построим схему графика функции 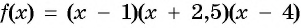 (рис. 83).
(рис. 83).
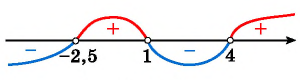
Рис. 83
При 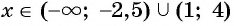 построенная кривая лежит ниже оси абсцисс. Это объединение интервалов является множеством решений данного неравенства.
построенная кривая лежит ниже оси абсцисс. Это объединение интервалов является множеством решений данного неравенства.
Ответ: 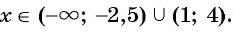
Решите неравенство
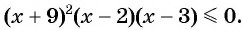
Решение:
Рассмотрим функцию 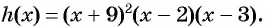 Найдем ее нули:
Найдем ее нули: 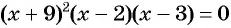 при
при 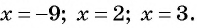 Так как неравенство нестрогое, то нули функции являются решениями данного неравенства, поэтому включим их во множество решений неравенства и отметим на оси абсцисс закрашенными точками (рис. 84).
Так как неравенство нестрогое, то нули функции являются решениями данного неравенства, поэтому включим их во множество решений неравенства и отметим на оси абсцисс закрашенными точками (рис. 84).
Затем определим положение графика функции в каждом из четырех полученных промежутков. Правее точки 3 каждый из трех множителей произведения 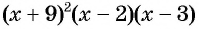 принимает положительные значения, значит, график функции расположен выше оси абсцисс. При переходе через точки 3 и 2 положение графика меняется, так как меняется знак одного из множителей
принимает положительные значения, значит, график функции расположен выше оси абсцисс. При переходе через точки 3 и 2 положение графика меняется, так как меняется знак одного из множителей 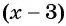 или
или 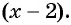 При переходе через точку -9 положение графика не меняется, так как множитель
При переходе через точку -9 положение графика не меняется, так как множитель 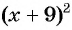 принимает неотрицательные значения при всех
принимает неотрицательные значения при всех 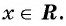
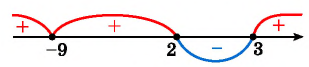
Рис. 84
Построим схему графика функции (см. рис. 84) и запишем решение неравенства в соответствии с его знаком: 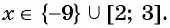
Ответ: 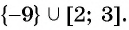
Если во множителе число 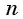 — четное, то при переходе через точку а положение графика относительно оси абсцисс не меняется, а если число
— четное, то при переходе через точку а положение графика относительно оси абсцисс не меняется, а если число 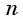 — нечетное, то меняется.
— нечетное, то меняется.
Больше примеров тут: https://www.evkova.org/drobno-ratsionalnyie-neravenstva
Дополнительный материал: https://www.berdov.com/docs/inequality/drobno-racionalnoe-neravenstvo/


Как Решать линейное неравенство
Основным способом решения таких неравенств сводится к равносильным преобразованиям для того, чтобы найти элементарные неравенства x < p (другие знаки), p являющееся некоторым числом, при а неравным нулю, а вида a < p (другие знаки) при a = 0.
Для решения неравенств с одной переменной , можно применять метод интервалов или изображать графически. Методы можно применять обособленно.








Пример решения графическим методом

Алгоритм решения:
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
Решаем так:
Перенести 1 из левой части в правую со знаком минус.
6х = 19 − 1
Выполнить вычитание.
6х = 18
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
х = 3
Ответ: 3.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.
Решаем так:
Раскрыть скобки
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
0х = 0
Ответ: х — любое число.
Линейное уравнение с двумя неизвестными
Определение
Уравнение вида , где
и
— неизвестные и свободный член
— любые действительные числа, называется линейным уравнением с двумя неизвестными.
— нормальный вид такого уравнения.
Каждая пара значений и
, удовлетворяющая уравнению с двумя неизвестными, называется решением этого уравнения.
Алгоритм решения:
1) если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
2) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.
Пример 1
Укажите три различных решения для уравнения 3x+y-2=0
Решение
Если x=0, то y=2; если y=0, то x=2/3; если x=1, то y=-1
Таким образом, пары чисел (0;2), (2/3;0), (1;-1) являются решениями данного уравнения. Заметим, что данное уравнение имеет бесконечно много решений. Для заданного значения x значение y=2-3x, т. е. любая пара чисел (x;2-3x), где x - любое число, является решением уравнения.
Больше примеров можно найти тут:https://zftsh.online/articles/5720
Называют данные уравнения - Биквадратные уравнения

Алгоритм решения


Метод разложения на множители
Решение уравнений, в которые переменная x входит с различными натуральными степенями и вещественными коэффициентами, по существу, является поиском корней многочлена.

Таким образом, разными способами находя корни и формируя скобки, можно постепенно добиваться понижения степени «оставшегося» многочлена, пока не будут найдены все корни.

Для разложения многочленов на множители применяются разные методы:
Метод замены переменной


При использовании метода замены переменной не забывайте возвращаться к исходной переменной.

Выделение полного квадрата
Метод выделения полного квадрата является одним из методов разложения на множители. Его идея – представить многочлен в виде разности квадратов двух других многочленов степенью пониже, и разложить разность на две скобки:

Такое разложение не всегда возможно.

Примеры:



Другие примеры можно посмотреть на сайте:
https://reshator.com/sprav/algebra/8-klass/reshenie-uravnenij-svodyashchihsya-k-kvadratnym/
Алгоритм решения
1.Раскрыть скобки, перенести все слагаемые в левую часть, чтобы уравнение приобрело вид: a*x^2 + b*x+c = 0
2.Выписать, чему равны в числах коэффициенты: a = ...
b = ...
c = ...
3.Вычислить дискриминант по формуле: D = b*b - 4*a*c
4.Если D = 0, будет один корень, который находится по формуле:
x = (-b)/2*a
5.Если D < 0, решений нет: x - пустое множество.
6.Если D > 0, будет два различных корня, которые находятся по формуле другой формуле, представленной на схеме.
Еще примеры можете найти тут : https://epmat.ru/kvadratnye-uravnenija/
Примеры решения:



Рациональное уравнение будет являться дробным в том случае, если одна или обе его части содержат дробь.
Дробно рациональные уравнения в обязательном порядке содержат деление на переменную или же переменная имеется в знаменателе. В записи целых уравнений такого деления нет.
1/x-1=x^3 и x:(5·x^3+y^2)=3:(x−1):5 – это дробно рациональные уравнения.
Алгоритм решения
Чтобы решить дробно-рациональное уравнение, нужно:


Рациональное уравнение – это такое уравнение, в обеих частях которого содержатся рациональные выражения.
Рациональное уравнение – это такое уравнение, запись левой части которого содержит рациональное выражение, а правая – нуль.
Рациональные уравнения точно также, как и уравнения других видов, могут содержать любое количество переменных от 1до нескольких. Для начала мы рассмотрим простые примеры, в которых уравнения будут содержать только одну переменную. А затем начнем постепенно усложнять задачу.
Рациональные уравнения делятся на две большие группы: целые и дробные. Посмотрим, какие уравнения будут относиться к каждой из групп.
Рациональное уравнение будет являться целым в том случае, если в записи левой и правой его частей содержатся целые рациональные выражения.
3⋅x+2=0 и (x+y)·(3·x2−1)+x=−y+0,5 – целые рациональные уравнения. Здесь обе части уравнения представлены целыми выражениями.
Алгоритм решения:
Примеры: Найдите х:


Другие примеры можно посмотреть тут:
https://myalfaschool.ru/articles/racionalnye-uravneniya-primery-resheniya
Одним из методов решения системы линейных уравнений с двумя переменными является метод сложения, рассмотрим его подробно.
Чтобы решить систему двух линейных уравнений с двумя переменными методом сложения необходимо следовать алгоритму.

Еще примеры есть тут: https://www.yaklass.ru/p/algebra/7-klass/reshenie-sistem-lineinykh-uravnenii-s-dvumia-peremennymi-10998/reshenie-sistem-lineinykh-uravnenii-metod-slozheniia-11000/re-bff14912-e902-4fdb-b0bb-3ad343066a70