par mccray fails Il y a 4 années
366
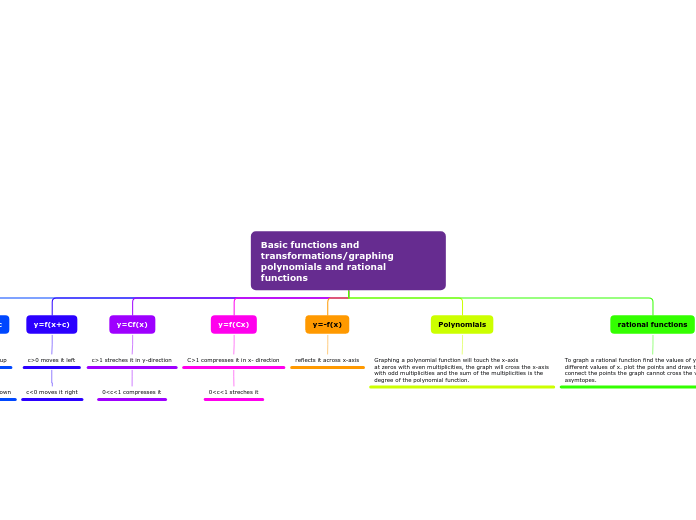
Basic functions and transformations/graphing polynomials and rational functions
par mccray fails Il y a 4 années
366

Plus de détails