par khang Han Il y a 4 années
464
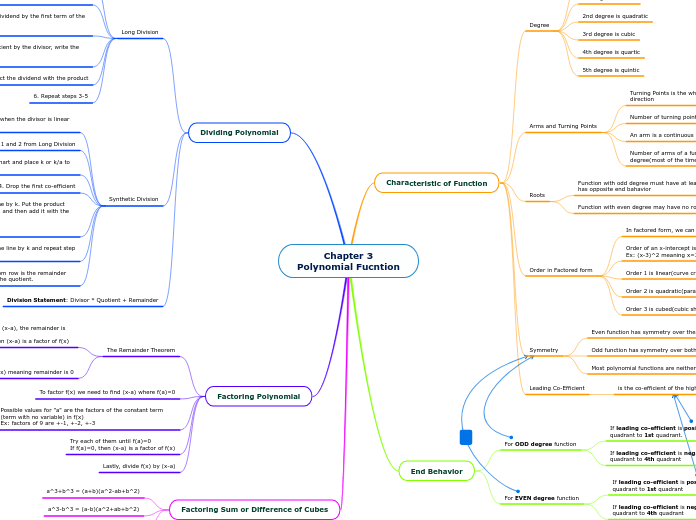
Chapter 3 Polynomial Fucntion
par khang Han Il y a 4 années
464

Plus de détails
x → +-∞, y → -∞
x → +-∞, y → ∞
x → -∞, y → +∞ x → +∞, y → -∞
x → -∞, y → -∞ x → +∞, y → +∞