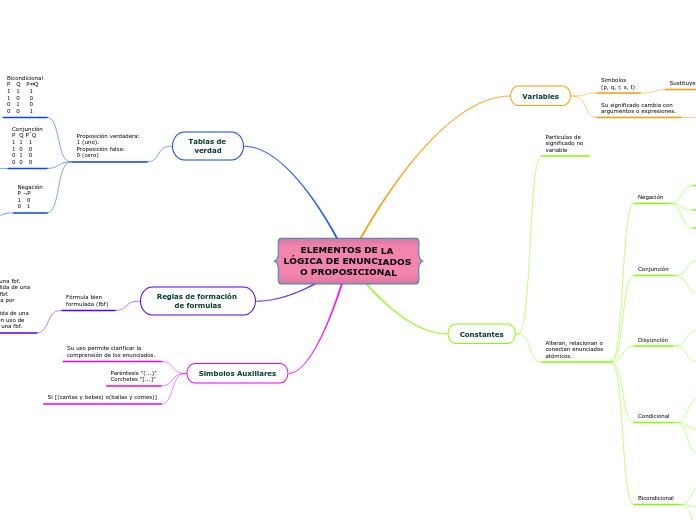
ELEMENTOS DE LA LÓGICA DE ENUNCIADOS O PROPOSICIONAL

Plus de détails

ESTADÍSTICA Ciencia que recoge, organiza, presenta, analiza e interpreta datos con el fin de propiciar una toma de decisiones más eficaz.

par Leonel Cabello

Partes invariables de la oración

par Josué Cortéz

Programacion

par Adolfo Mario Viloria Corro

Sample Mind Map

par CRISTIAN CHUQUIN

ELEMENTOS DE LA LÓGICA DE ENUNCIADOS O PROPOSICIONAL

Simbolos Auxiliares

Si [(cantas y bebes) o(bailas y comes)]

Paréntesis "(...)" Corchetes "[...]"

Su uso permite clarificar la comprensión de los enunciados.

Reglas de formación de formulas

Fórmula bien formulada (fbf)

1. Una variable proposicional es una fbf. 2. Una fbf precedida de una negación es una fbf. 3. Una fbf seguida por cualquiera de las constantes, seguida de una fbf, haciendo buen uso de los paréntesis es una fbf.

Tablas de verdad

Proposición verdadera: 1 (uno). Proposición falsa: 0 (cero)

Negación P ¬P 1 0 0 1

Disyunción P Q P˅Q 1 1 1 1 0 1 0 1 1 0 0 0

Conjunción P Q P˄Q 1 1 1 1 0 0 0 1 0 0 0 0

Condicional P Q P⇒Q 1 1 1 1 0 0 0 1 1 0 0 1

Bicondicional P Q P⇔Q 1 1 1 1 0 0 0 1 0 0 0 1

Constantes

Alteran, relacionan o conectan enunciados atómicos.

Bicondicional

p: Es de noche. q: Se ha ocultado el Sol. p ↔ q "Es de noche si y sólo si se ha ocultado el sol".

Indica doble condición, equivale, cuando y solo cuando

Condición necesaria y suficiente

Se simboliza con: ↔ (También:≡ )

Representa las partículas lingüísticas si y sólo si…

Condicional

p: Llueve q: La tierra se moja. p → q "Si llueve, entonces la tierra se moja".

"cuando...entonces..., entonces o una simple "coma" (,)

"entonces" o "equivalente" separa el antecedente del consecuente.

Se simboliza con: → (También: ⊃ )

Representa las partículas lingüísticas si p entonces..q

Disyunción

Tiene dos sentidos: uno inclusivo y otro exclusivo.

p: Se aprende lógica escuchando la clase. q: Se aprende lógica estudiando p ˅ q "Se aprende lógica escuchando la clase o estudiando"

Se simboliza con: ˅= (o)

Representa la partícula lingüística "o"

Conjunción

Indica la idea de unión (también, igualmente, pero).

p: Marte tiene satelites. q: Jupiter tiene satélites. p ˄ q "Marte tiene satélites y Júpiter también".

Se simboliza con: ˄ (También: ·, & ) = y

Representa la partícula lingüística "y"

Negación

¬p: La luna no tiene satélites. p: La luna tiene satélites.

"No es el caso que, no pasa que, ni, etc."

¬p, ¬q, ¬r, ¬s, t¬.

Se simboliza con: ¬. (También: - , ~)

Representa la partícula lingüística "no" u otras con la idea de negación.

Particulas de significado no variable

Variables

Su significado cambia con argumentos o expresiones.

Ejemplo: p= La Tierra es un planeta.

Simbolos (p, q, r, s, t)

Sustituyen proposiciones o enunciados.