par Tanreet Dharni Il y a 4 années
351
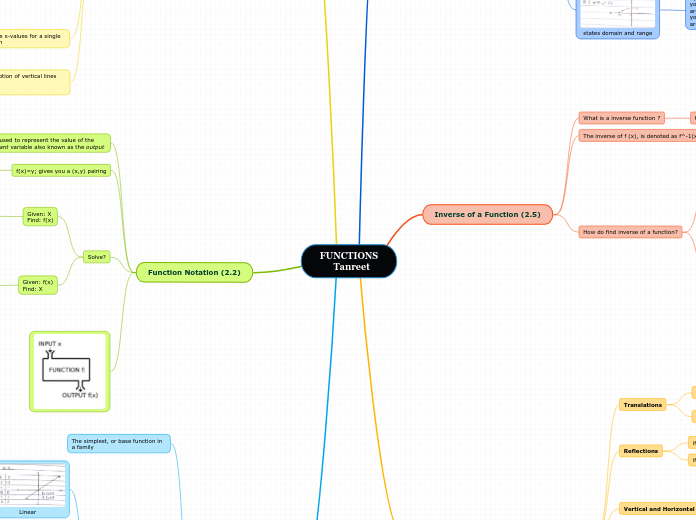
FUNCTIONS Tanreet
In mathematics, a function is a special type of relation where each input is associated with exactly one output. The independent variable, or domain, consists of all possible values of x, while the dependent variable, or range, includes all possible values of y.