MÉTODOS DE RESOLUCION DE SISTEMAS DE ECUACIONES

Plus de détails

Las preferencias

par Maria Alejandra Rodriguez

MEDIDORES DE CAUDAL

par Sahira Alejandra Amador

resolucion 1536 de 2015

par claudia tibaduiza

INTEGRALES

par Pedro Amaya

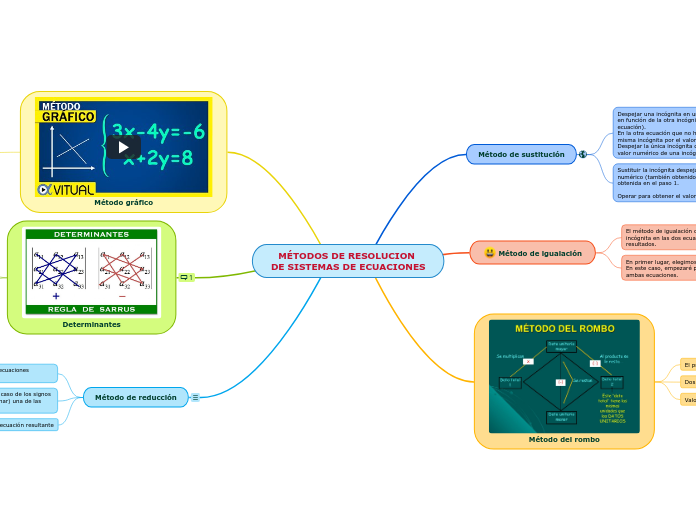
MÉTODOS DE RESOLUCION DE SISTEMAS DE ECUACIONES

Método de reducción

El método de reducción consiste en operar con las ecuaciones como, por ejemplo, sumar o restar ambas ecuaciones, de modo que una de las incógnitas desaparezca.

Se resuelve la ecuación resultante

Realizamos una resta (o suma según sea el caso de los signos de los coeficientes) para desaparecer (eliminar) una de las incógnitas

multiplicándolas por un numero tal que las ecuaciones resultantes tengan un coeficiente en común

Determinantes

El Método de determinantes es una forma de resolución de sistemas de ecuaciones lineales, al igual que los métodos sustitución e igualación, este método permite obtener el resultado de un sistema de ecuaciones en unos simples pasos

El paso siguiente es aislar los coeficientes de las incógnitas a, b y c en el orden en que aparecen para hallar la solución al sistema

Se emplea este método cuando las ecuaciones del sistema poseen coeficientes, vamos a considerar el siguiente sistema:

Método gráfico

Por tanto, cada una de las ecuaciones que forman un sistema corresponde a la ecuación de una recta, por lo que podemos representar cada una de ellas en los ejes cartesianos y el punto de corte de ambas rectas corresponderá a la solución del sistema de ecuaciones.

Método del rombo

Valor unitario de cada una de las incógnitas.

Dos cantidades totales:

El problema debe tener 2 incógnitas.

Método de igualación

En primer lugar, elegimos la incógnita que deseamos despejar. En este caso, empezaré por la «x» y despejo la misma en ambas ecuaciones.

El método de igualación consiste en despejar la misma incógnita en las dos ecuaciones y después igualar los resultados.

Método de sustitución

Sustituir la incógnita despejada en el paso 3 por su valor numérico (también obtenido en el paso 3) en la ecuación obtenida en el paso 1. Operar para obtener el valor numérico de la otra incógnita

Despejar una incógnita en una de las ecuaciones, que quedará en función de la otra incógnita (seguiremos teniendo una ecuación). En la otra ecuación que no hemos utilizado, se sustituye la misma incógnita por el valor obtenido en el paso 1. Despejar la única incógnita que nos quede. Obtenemos el valor numérico de una incógnita.