par Gabriella Alford Il y a 6 années
400
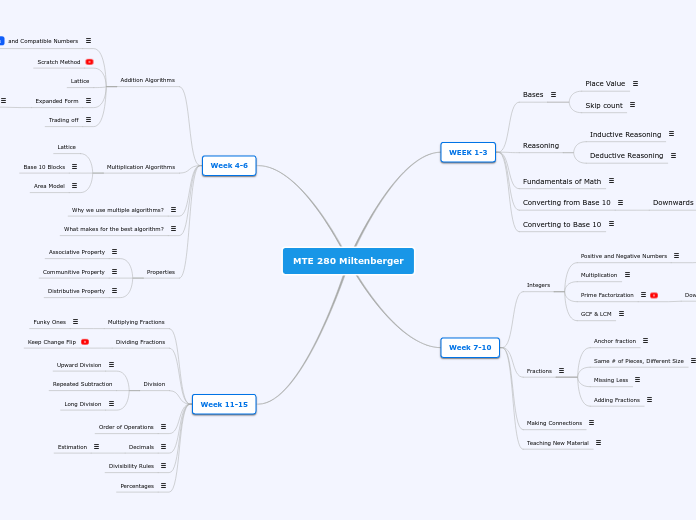
MTE 280 Miltenberger
par Gabriella Alford Il y a 6 années
400

Plus de détails
80% of 40
10% = 4
x 8 x 8
__________
80% = 32
100%
-
70% discount off of $80
_____
30% of $80
10% = 8
x 3 x 3
____________
30% = $24
2 - Last # is even
3 - Sum of digits can be divided by 3
4 - Last 2 numbers can be divided by 4
5 - Last # is 0/5
6 - If 2 and 3 work then six works
8 - Last 3 numbers can be divided by 8
9 - Sum of digits can be divided by 9
10 - Last number is 0
Groups
(2, 5, 10)
(3, 9)
(2, 3, 6)
(2, 4, 8)
Line up the whole numbers, add 0's so it will still always work (subtraction).
Always shown a rectangle with 10 longs in it.
2 x 3 = 6
2.14 x 3.6 =
214
x 36
_______
7704
we know that the whole numbers multiplied together equals 6 so the most realistic answer we could do is 7.704
G roups
E xponents
M ultiply/ D ivide ---->
A ddition/S ubtraction ------>
M/D and A/S move left to right
In any problem find the + and -
Draw lines going down which break up the problem and allows you to do G, E, M/D.
Then add left to right
BAD
worst way to divide
not even worth putting info about
Emphasizes place value requires student to be able to estimate though.
243 / 6
24 -24 = 0
243 3
_______ = 40 _____
6 6
4 15
____ x _____
9 22
2 x 2 3 x 5 2 x 2 x 3 x 5
_____ X ______ = ____________
3 x 3 2 x 11 2 x 3 x 3 x 11
You draw a long 1 across through numbers that would equal 1.
So a 2 in the numerator and a 2 in the denominator would be 1 so you you'd draw a long funky through those numbers, along with the one 3 in the numerator and one 3 in the denominator.
3 (x + 4)
3 + 4 + 7 = 3 + 7 + 4
(3+4) + 7 = 3 + (4+7)
Efficiency and Place Value
-To show students the fundamentals of adding or multiplying then can teach them short cuts.
-Some algorithms might be easier or quicker for certain students.
-Some may not be as efficient
-In some situations, using one algorithm versus another can be more useful or helpful in a certain situation.
Based off of the base 10 blocks model but is quicker and more efficient not making us have to break down every single unit and or long to get an answer.
Ex.
13 x 15
10 + 3
__________________
| |
10 | |
| 100 | 30 100
+ |_________|________ 30
| | 50
5 | 50 | 15 15
|_________|________ --------
195
A model we use to show place value and allow a student to draw out every flat, long, and unit that makes up a number when multiplied together.
Putting numbers in a vertical line and borrowing from one of the numbers to make 0 in the ones place and add 1 to the tens place.
Ex.
48 +2 50
+27 -2 + 25
---------- -----------
75 75
Expanding the numbers to be able to see place value.
Ex.
428 400 + 20 + 8
+ 56 50 + 6
----------- ----------------
484 400 +70 + 14
484
Left to Right
Taking expanded to the next level and writing out place value but doing it from left to right skipping a line every time you go to a new place value.
Ex:
572
+ 324
----------
800
90
6
----------
896
A method to use when adding by trying to find numbers that add to 10 or result in so many longs and no units left over. Numbers that are compatible and equal to a tens place.
Ex:
32 + 16 + 48 + 11 + 34 + 44 + 45
30 + 20 + 50 + 10 + 40 + 50
Start with a manipulative
Draw representation (show)
Move to algorithms (algebra)
The most important thing when teaching someone and something is making connections that can apply to other aspects of life, problems, classes etc.
3 <------ how much you have
_____
7 <------ size of the piece
Denominators are counter intuitive
Draw same size boxes for each fraction
1 box vertical and 1 box horizontal (lines)
Transpose and make them the same size by adding the lines vertical and horizontal to each
(addition, make 3rd box and add all pieces)
(subtraction, take away however many boxes by writing and x)
then draw answer and write
Drawing gives us a common denominator
13/14 < 16/17
6/11 > 6/13
7/13 > 11/23
emphasizes 1/2
Greatest Common Factor: small #
Least Common Multiple: big #
18 2 |_20__
3 6 5 |_10__
2 3 2
2 x 3^2 2^2 x 5
GCF = 2
LCM = 2^2 x 3^2 x 5
Prime: 2 factors
Composite: More than 2 factors
The # 1 is neither
We use a factor tree for prime factorization
We use PF to be able to find commonalities between numbers
Downward Division
Another way to find the prime factorization
2 |_32__
2 |_16__
2 |_8__
2 |_4__
2 |_2_
2^5
2 |_28__
2 |_14__
2 |_7__
2^3 x 7
First number is the # of groups
Second number is how many is inside of the groups
Circles represent groups
2(3) -- 2 groups of 3
+ + + +
+ +
-2(3)
+ + + + + +
_ _ _ _ _ _
0 take away 2 groups of 3
*circle 6 positive and you are left with 6 negatives = -6
Zero pair:
+
_
Start with any number you want and how ever many you need
Positives on the top
Negatives on the bottom
Group of zero pairs = zero bank
If the signs are the same the answer is positive
If the signs are different then the answer is negative
Ex.
-5 using 9 tiles
+ +
_ _ _ _ _ _ _
8 using 10 tiles
+ + + + + + + + +
_
4 + (-5)
+ + + +
_ _ _ _ _
Keep Change Change
12 + (-20)
+ _ _
circle the positive and negative and subtract 12 from 20 and put a negative sign
When converting from any base to base 10 we can draw it out or solve it with an algorithm.
Ex. 321 base 6 to base 10
FLAT FLAT FLAT LONG LONG UNIT
3 flats 2 longs 1 unit
OR
3 (6^2) + 2(6^1) + 1(6^0)
starting at the number farthest right, we use the exponent 0 and as we go up each place we add 1 to the exponent
for the number 236581 base 9 to base 10 we would do
2(9^5) + 3(9^4) + 6(9^3) + 5(9^2) + 8(9^1) + 1(9^0)
and find the sum
Converting from base 10 we can draw it out by skip counting and using tallies, but if the numbers get too big then we can use downward division.
When you are leaving base 10 and going to a different base
Ex.
243 to base five
5 L243__|
5 L48_ | 3
5 L9_ | 3
1 | 4
The number would be 1433 base five
10 frames often used, look like longs
Using prior knowledge to recognize something
Noticing that there is a pattern
Bases can only have one symbol so for anything more than 9 we use 2 symbols.
Example:
8
9
T
E
W
If we don't write the bases we assume it is in base 10
When changing from base 10 to another base, rather than counting 1 2 3 4 5 6 7 all the way to say for example 56 instead be can go
7 14 21 28 35 42 49 56 and know that we have 6 "longs" because to fill a long we need 7 units which we included by skip counting.
Units- 1
Longs- 10
Flats- 100
The long names the base, however many units fit in a long tells us how big the base is.
The numbers in each place value must be smaller than whatever base it is in.