par Milagros Noriega Il y a 2 années
497
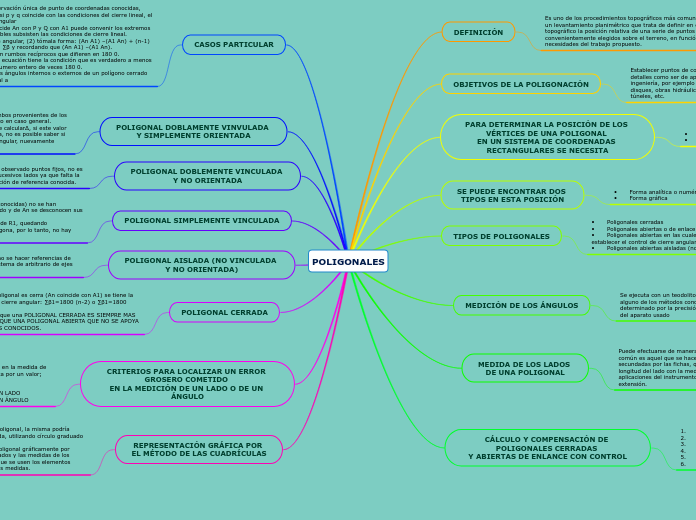
POLIGONALES
La poligonación es una técnica esencial en topografía que se centra en la medición y cálculo de ángulos y distancias entre puntos de control. Se utilizan instrumentos como teodolitos o estaciones totales para medir ángulos múltiples veces, dependiendo de la precisión requerida.