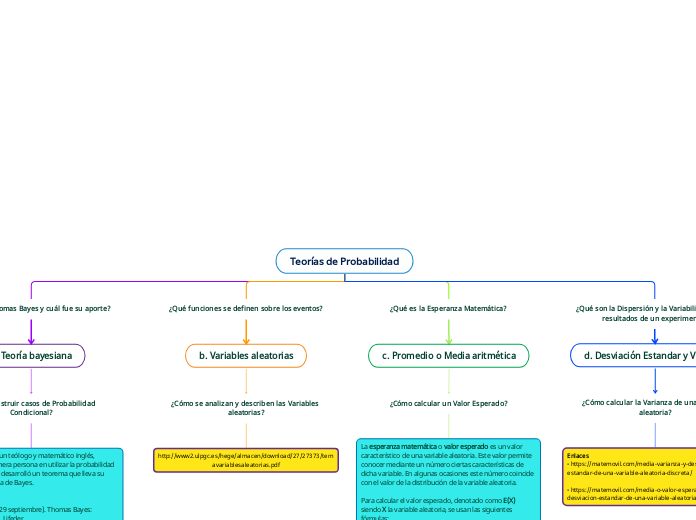
Teorías de Probabilidad

Plus de détails

fisica cuantica 2

par daniel siachoque

Evaluación de las cadenas musculares en el deportista

par John Alexander Pistala

Probabilidad de respuesta

par Maikol Guzman

EL Estrabismo

par Geraldine V

Teorías de Probabilidad

¿Qué son la Dispersión y la Variabilidad de los resultados de un experimento?

d. Desviación Estandar y Varianza

¿Cómo calcular la Varianza de una variable aleatoria?

Enlaces - https://matemovil.com/media-varianza-y-desviacion-estandar-de-una-variable-aleatoria-discreta/ - https://matemovil.com/media-o-valor-esperado-varianza-y-desviacion-estandar-de-una-variable-aleatoria-continua/

¿Qué es la Esperanza Matemática?

c. Promedio o Media aritmética

¿Cómo calcular un Valor Esperado?

La esperanza matemática o valor esperado es un valor característico de una variable aleatoria. Este valor permite conocer mediante un número ciertas características de dicha variable. En algunas ocasiones este número coincide con el valor de la distribución de la variable aleatoria. Para calcular el valor esperado, denotado como E(X) siendo X la variable aleatoria, se usan las siguientes fórmulas: - Si la variable X es discreta: E(X) = ∑ Xi P(Xi) - Si la variable X es continua: E(X) = ∫ Xi P(Xi) dX (la integral tiene por limite inferior - ∞ y por limite superior +∞) Donde Xi son cada uno de los valores de la variable aleatoria y P(Xi) es la probabilidad correspondiente. Adaptado de: - Rustom, A. (2020). Estadística descriptiva, probabilidad e inferencia. https://repositorio.uchile.cl/bitstream/handle/2250/120284/Rustom_Antonio_Estadistica_descriptiva.pdf?sequence=1&isAllowed=y - Walpole, R. E. (2012). Probabilidad Y Estadística Para Ingeniería Y Ciencias (9.a ed.). PEARSON EDUCACION. https://vereniciafunez94hotmail.files.wordpress.com/2014/08/8va-probabilidad-y-estadistica-para-ingenier-walpole_8.pdf

¿Qué funciones se definen sobre los eventos?

b. Variables aleatorias

¿Cómo se analizan y describen las Variables aleatorias?

http://www2.ulpgc.es/hege/almacen/download/27/27373/temavariablesaleatorias.pdf

¿Quién fue Thomas Bayes y cuál fue su aporte?

a. Teoría bayesiana

¿Cómo construir casos de Probabilidad Condicional?

Thomas Bayes fue un teólogo y matemático inglés, considerado la primera persona en utilizar la probabilidad inductiva. Además, desarrolló un teorema que lleva su nombre: el Teorema de Bayes. Ver más en: - Ibarra, M. (2018, 29 septiembre). Thomas Bayes: Biografía y Aportes. Lifeder. https://www.lifeder.com/thomas-bayes/ La Probabilidad Condicional es aquella que resulta de buscar la probabilidad de un evento, llamémoslo A, que depende de un evento que ha sucedido con anterioridad, nombrémoslo B. Para realizar el cálculo de dicha probabilidad, notada como P(A|B), se utiliza la siguiente fórmula: P(A|B) = P(A∩B) / P(B) Donde: - P(A∩B) es la probabilidad de que ocurra el evento A y el evento B. - P(B) es la probabilidad de que ocurra el evento B. Ejemplo: En una escuela se hizo un estudio y se encontró que: el 20% de los alumnos son buenos estudiantes, 30% son buenos deportistas y un 5% son buenos en ambas cosas, entonces ¿Qué probabilidad hay de que al seleccionar un alumno que sea buen deportista, también sea buen estudiante? Sea: - P(A) = 20 = 0,2 - P(B) = 30 = 0,3 - P(A∩B) = 5 = 0,05 Entonces la probabilidad de que al seleccionar un estudiante bueno en deportes, también sea buen estudiante es: P(A|B) = 0,05 / 0,3 = 0,166 = 16,6% Adaptado de: - Probabilidad condicional. (s. f.). Fhybea. https://www.fhybea.com/probabilidad-condicional.html