Basic geometry and polygons

Triangles

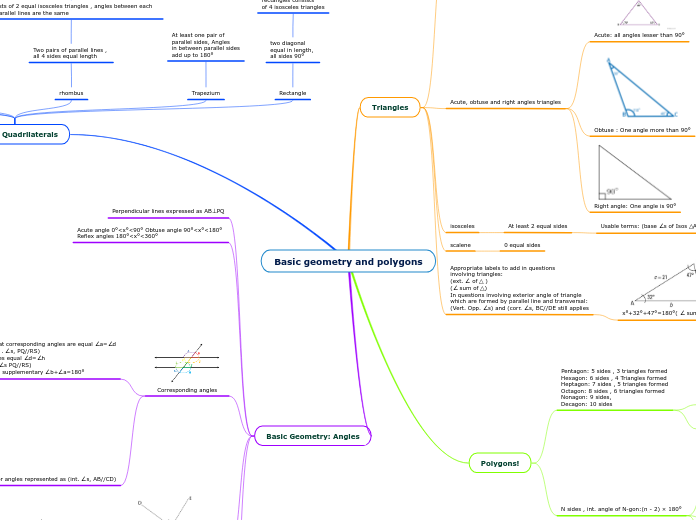
Equilateral triangles

All angles are 60° , all sides equal length

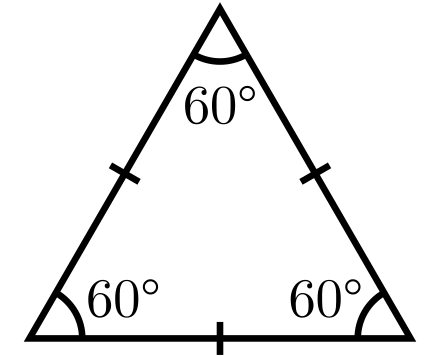
Acute, obtuse and right angles triangles

Acute: all angles lesser than 90°

Acute: all angles lesser than 90°

Obtuse : One angle more than 90°

Obtuse : One angle more than 90°

Right angle: One angle is 90°

Right angle: One angle is 90°

isosceles

At least 2 equal sides

Usable terms: (base ∠s of Isos △ABD

scalene

0 equal sides

Appropriate labels to add in questions
involving triangles:
(ext. ∠ of △ )
(∠ sum of △)
In questions involving exterior angle of triangle
which are formed by parallel line and transversal:
(Vert. Opp. ∠s) and (corr. ∠s, BC//DE still applies

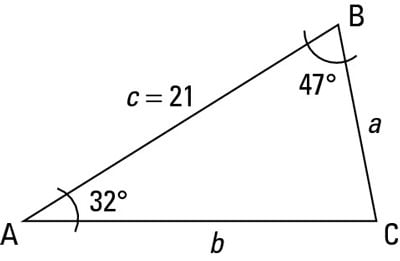
x°+32°+47°=180°( ∠ sum of △)

x°+32°+47°=180°( ∠ sum of △)

Polygons!

Pentagon: 5 sides , 3 triangles formed
Hexagon: 6 sides , 4 Triangles formed
Heptagon: 7 sides , 5 triangles formed
Octagon: 8 sides , 6 triangles formed
Nonagon: 9 sides,
Decagon: 10 sides

sum of interior angles
Pentagon:540°
Hexagon: 720°
Heptagon: 900°
Octagon: 1080°
Nonagon: 1260°
Decagon: 1440°
Formula :int. angle=(n - 2) × 180°

exterior angle of a polygon
= 360 ÷ number of sides.

N sides , int. angle of N-gon:(n - 2) × 180°

Sum on int. angles in a decagon
Decagon:10 sides
Sum of int angles: (nx2)× 180°

Finding no. of sides in regular polygon
if interior angle is given as°162°
(n-2)x180°/n= 162°
(n-2)x180°=162° x n
180n-162n=360
18n=360
n=20

Problem involving regular polygons with unknown no. of sides
Finding no. of sides using exterior angles of n-sided polygon
Sum of ext. angles=360°
Given size of each ext. angle: 24°
n=360°/24°=15

Special Quadrilaterals

square

parallelogram

Two pairs of parallel lines ,
diagonals bisect each other ,
angles in between add up to 180°

kite

At least 2 pairs of adjacent sides

consists of two isosceles triangles , one smaller than the other

consists of two isosceles triangles ,
one smaller than the other

∠DEA=∠DEC(longer diagonal BD bisects ∠ADC)
=25°
∠DEC°=90° ( diagonals of kite cut each other at
right angles)
∠BAD=∠BCD(opp. ∠s of kite)

rhombus

Two pairs of parallel lines ,
all 4 sides equal length

Consists of 2 equal isosceles triangles , angles between each two parallel lines are the same

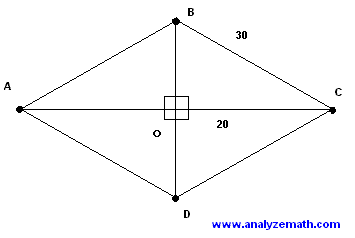
Take ∠ADO to be 68°
∠CBD=∠ABD(diagonal BD of rhombus
bisects ∠abc)
∠AOB=90°(Diagonals of rhombus
bisect each other at right angles)

Trapezium

At least one pair of
parallel sides, Angles
in between parallel sides
add up to 180°

Rectangle

two diagonal
equal in length,
all sides 90°

rectangles consists
of 4 isosceles triangles

Usable terms:Int. ∠ of rect.)

Basic Geometry: Angles

Perpendicular lines expressed as AB⊥PQ

Acute angle 0°<x°<90° Obtuse angle 90°<x°<180°
Reflex angles 180°<x°<360°

Corresponding angles

Corresponding angles

This means that corresponding angles are equal ∠a=∠d
Example (Corr . ∠s, PQ//RS)
Alternate angles equal ∠d=∠h
Example (Alt. ∠s PQ//RS)
Interior angles supplementary ∠b+∠a=180°

Z angle can be applied to find the other
of corresponding angle

Example of corresponding angle question where a=55° as alt. ∠s is applicable

Example of corresponding angle question
where a=55° as alt. ∠s is applicable

This also consists of two pairs of parallel lines . a line QP will have to be drawn horizontally in between angle x in order

This also consists of two pairs of parallel
lines . a line QP will have to be drawn horizontally in between
angle x in order to get two Z angles , where reflex of angle x
= w+z ( Alt.∠s , AA//QP) ( Alt ∠s CC//QP)

Interior angles represented as (int. ∠s, AB//CD)

Adjacent angles on a straight line, Represented as (Adj. ∠s on a str. line)

Adjacent angles on a straight line,
Represented as (Adj. ∠s on a str. line)

180°= x + 3x + 2x (adj. ∠s on a str. line)

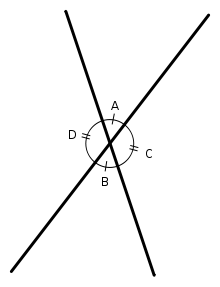
Vertically opposite angles occurs when straight lines intersect

Vertically opposite angles occurs when straight lines intersect

A=B (vert. opp. ∠s)