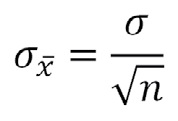Capitulo 8. Métodos de muestreo y teorema
central del límite
Razones para muestrear
Cuando se estudian las características de una población, existen diversas razones prácticas para preferir algunas partes (o muestras) de esta para observar y medir
1. Establecer contacto con toda la población requiere mucho tiempo.
2. El costo de estudiar todos los elementos de una población resulta prohibitivo.
3. Es imposible verificar de manera física todos los elementos de la población.
4. Algunas pruebas son de naturaleza destructiva.
5. Los resultados de la muestra son adecuados.
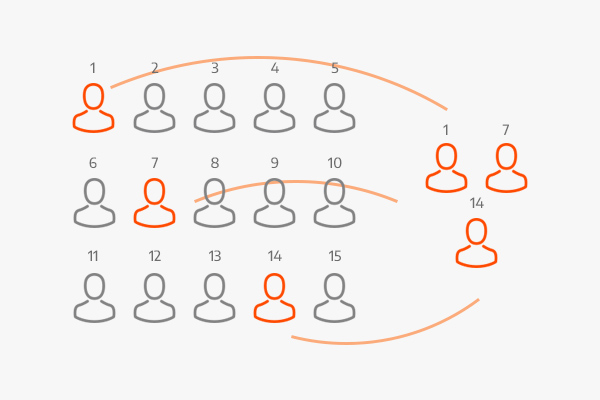
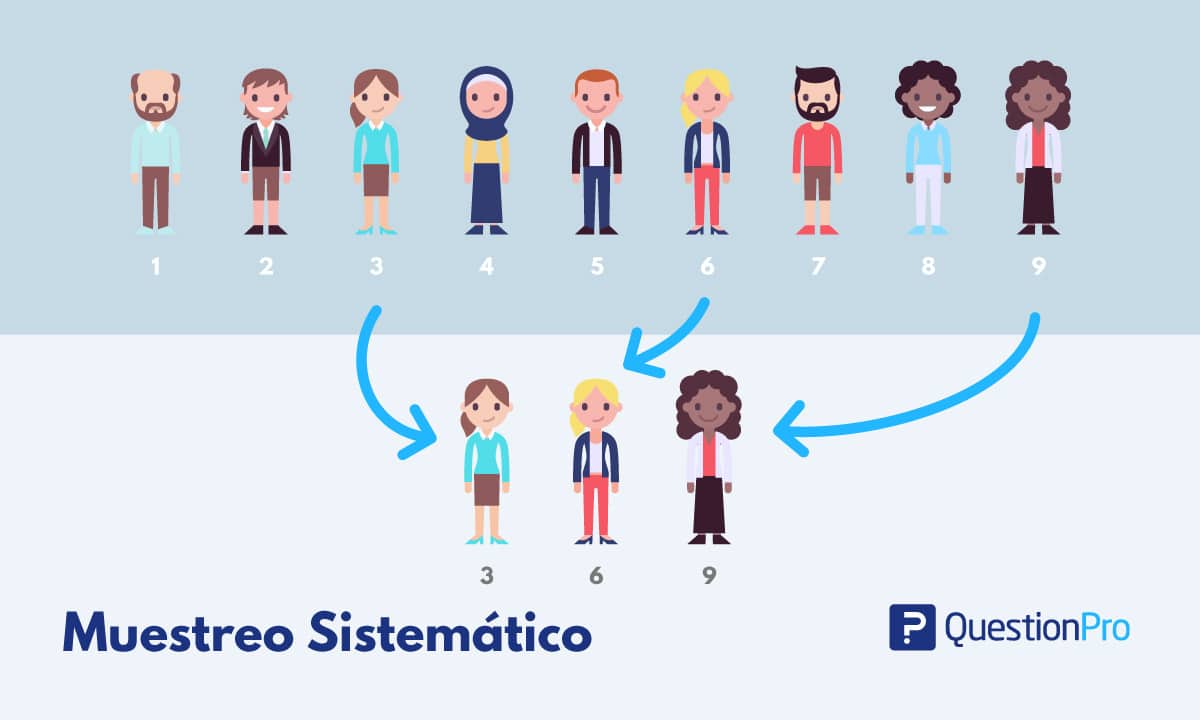
Muestreo aleatorio sistemático
Se selecciona un punto aleatorio de inicio y posteriormente se elige cada k-ésimo miembro de la población.
El muestreo aleatorio simple se utiliza para seleccionar los días, los horarios y el punto de partida; pero el procedimiento sistemático se emplea para seleccionar al cliente real.
Muestreo aleatorio estratificado
Una población se divide en subgrupos, denominados estratos, y se selecciona al azar una muestra de cada uno.
Elmuestreo aleatorio estratificado garantiza que cada grupo o estrato se encuentre representado en la muestra.
Muestreo por conglomerados
La población se divide en conglomerados a partir de los límites naturales geográficos u otra clase. A continuación, estos se seleccionan al azar y se toma una muestra de forma aleatoria con elementos de cada grupo.
Este es otro tipo común de muestreo; a menudo se emplea para reducir el costo de muestrear una población dispersa en cierta área geográfica.
Muestreo aleatorio simple
Muestra seleccionada de manera que cada elemento o individuo de la población tenga las mismas posibilidades de que se le incluya.
Teorema central del límite
Si todas las muestras de un tamaño en particular se seleccionan de cualquier población, la distribución muestral de la media se aproxima a una distribución normal; esta mejora con muestras más grandes
El teorema central del límite hace hincapié en que, en el caso de muestras aleatorias grandes, la forma de la distribución muestral de la media se aproxima a la distribución de probabilidad normal. La aproximación es más exacta en el caso de muestras grandes que en el de muestras pequeñas; lo cual es una de las conclusiones más útiles de la estadística porque permite razonar sobre la distribución de las medias muestrales sin ninguna información acerca de la forma de la distribución de la población de la que se toma la muestra.
Distribución muestral de la media
Distribución de probabilidad de todas las posibles medias de las muestras de un determinado tamaño muestral de la población.
Si se organizan las medias de todas las muestras posibles de 5 días en una distribución de probabilidad, el resultado recibe el nombre de distribución muestral de la media.
“Error” de muestreo
Diferencia entre el estadístico de una muestra y el parámetro de la población correspondiente.
es poco factible que la desviación estándar de la muestra sea exactamente igual a la de la población; por lo tanto, se puede esperar una diferencia entre un estadístico de la muestra y el parámetro de la población correspondiente; la cual recibe el nombre de error de muestreo.