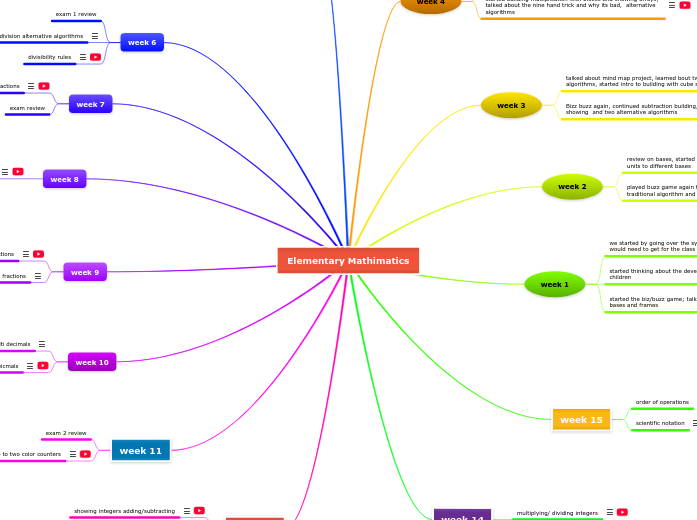
Elementary Mathimatics

it important that kids know that 4(7) is different from 7(4) they have the same answer but one is four groups of seven and the other seven groups of four!models: groupsarraysarea

the nines are bad because it doesn't help the fins patterns and wont help them understand higher math alternative algorithm:expanded form left to rightarea modellattice

the two alternative algorithms: expanded form very similar to addition expanded from and equal addends

traditional algorithm not based of prior knowledge and confusing for some students. alternative algorithms:expanded form, left to right, friendly numbers/trading off,scratch, lattice

(early number sense) Cardinality, when they finish counting a group they will know how many are in that group with out needed to count a again. one to one correspondence: each number goes with one item they are touchingcounting more and less, subitizing: they can look at a group and tell how many are in it just by looking at it without counting. . then a basic intro to bases.cube, long, flat, cube, long, flatone, ten, hundred,

frames are used when a students fills it up usually with block and it counts to ten a five is used a stepping stool to then ten frame, there are different bases, normal every day bases are base 10. base 5 is when you have five units it makes one long five longs make a flat etc..

shows how to tell the sign of exponents add a zero!examples0-4^2=0-8=-160+(-4)^2=0+16=160-(-4)^2 =0-16=-16order of operations:NO p e m d a s!also not horizontal go verticalGroups ExponentsM/D from L-> RA/S from L -> Rgroups go along with parenthesis and are separated by addition and subtraction symbolsA) -4+7(2)-8^2group -4= -4group 7(2)= 14group 8^2 =64 left to right-4+14= 1010-14= -4-4 answer!

scientific notation:the decimals need to be between 1-10negative exponent = very small numberpositive exponent = very big numberstandard form number bigger than 1 = positive exponentstandard form number written as decimal = negative exponent2.15x10^-4 = small number/ decimal5.873 x 10^6 = big number0.000467 = neg exp4.67x10^-43470000= pos exp3.47x10^6

show :create groups for positive create circles then add in the symbols for the integers insidetotal them up for answerfor negative do same as before with add/subtract create zero pairs and group up the symbols then arrows for taking away. left over is answermultiplication and division: (negative and negative NOT equal to positive)neg times neg = positive!same sign answer is positivedifferent sign answer is negativeexample-60(30)different sign = neg60(30)=1800-1800 answer!(same for division)

Automaticity is the ability to do things without occupying the mind with the low-level details required, allowing it to become an automatic response pattern or habit. It is usually the result of learning, repetition, and practice.your start with "red" easy ones 1,2,5,10 "blue" medium 3,9,doubles (4(4))"green" hard 4,6,7,8

equal addends: both number add up to a friendly number so you don't have to carry

trad division: Students will have a hard time knowing where numbers goes( big # not on the outside) repeat sub:figure out the highest the student knows of the factors and write it on the side then subtract and keep repeating. Remainder goes in the numerator and the outside number is the denominator. PRO: students can start with what they have/know and be motivated to do faster. CONS: write it wrong and difficulty what to do with the remainder. up division:Write the equation how you say it just vertically (like a fraction). Writing the numbers spaced out to be able to write other numbers in between. Figure out how many times the denominator can go into the numerator; write in answer spot. Then multiply it to subtract from the first digit then divide again for the next digit. Remainder is the numerator and the denominator stays the same. CON: student needs to be good at math facts.

divisibility rules: help learn what number are factors for high level math2 even #send in 0,2,4,6,83the sum of the digits is / by 34if the last 2 digits are / 4 then yes 5last digit is 5 or 06if 2 and 3 work 6 works8 if last 3 digits /9 the sum of digits / 910 last digits is 0

numerator = number pieces havedenominator = how many pieces total/size of piecesstarted comparing: which fraction is bigger, smaller, or equal(1/2 helps)(anchor fractions)(butterfly method)multiply numerator by 2ex: 7/13 or 11/237(2)= 14 more than 1311(2)= 22 less then 23

building: place on top of each other for both add and subadd:(improper fractions)multiply then add circles for each whole numberpie divide into for fraction partfor both add and sub (need both denominator to be same in order to do problem)show:use rectangles to show: 3 recuse rectangles to show : 2rec

Adding whole numbers to fractions: you just combine the two for your answer.Subtracting whole number from a fraction: you will need to make the whole number into a mixed number with the same denominator as the fraction.Subtracting mixed number by mixed number: you subtract whole numbers first then multiply to get same denominator, then subtract.Adding mixed numbers with mixed numbers: you add whole numbers together then work on finding the same denominator; then add.Multiplying fraction by fraction: work with numerator to denominator to find factors for Funky 1 to simplify, then multiply across.Mixed number multiplied by mixed number: Do the backwards "C" to multiply denominator by whole number then add to numerator. Then funky 1.Dividing fraction by fraction: use KEEP, CHANGE, FLIP (multiply by the reciprocal),

circle fractions are easiest to understand but you need to change to rectangle for bigger ones so students don't get confused.set model: name items (color ,shape , etc.)1/3 is blue8/10 are circleslength model: size, length comparisonpencil 1/2 longer penjohn 2/5 the height of Emilyarea model: fraction to area comparison (on top)red 1/2 of yellowpurple is 2/3 green

showing:uses squares cuts them up , each long is a tenth each cube a hundredth add:put them together, divide them up in one square and add them up vertical tenth horizonal hundredthsub:same principles as addition but instead of adding them up divide the first one them circle the amount of the second one and "take away"multiply:same thing as add and sub but your gonna overlay them the parts that are overlaid by both are the answer. vertical first number horizontal second number

Add whole numbers: combine the twoSub whole number: whole number to mixed number (denominator same fraction)Sub mixed mixed: sub whole first multiply denominator for same, then subtract.Add mixed mixed: add whole first, same denominator; then add.Multi: find factors for funky 1 for simplify, multiply across.Mixed by mixed: backwards "C" multi denom by whole, add to num (funky 1 last)Divide: keep change flip (multiply by the reciprocal)

two color counters:help build integers red = negativeyellow/ other color ( not red) = positiveyellows on top because positive always goes on topred on bottom because negative always goes belowzero bank: a positive and negative together (or multiple)

adding show:example:-3+(-5) - - - - - - - -= -8example :3+(-2)(+ +) + (- - )= 1 underline startingblue answerred adding/subtractingadd in the negatives or positives as you need then subtracting show: example-3-(-4) +(+)<~ - - - - (-)zero pairs: if you don't have enough to subtract add in some zeros! and create a zero bank for the extras

SOLVEinteger adding :example-6+(-4)6 is bigger (bigger group) - -4 is smaller (smaller group) -6+4=10-10 answer!circle twodifferent symbols = subtractsame symbols = additionsymbol left over is sign for answer (negative or positive)Hectors methodinteger subtracting:example-8-(-4)KCC!keep change changekeep -8change the subtraction to additionchange -4 to positive 4 -8+4-8 bigger group - -4 smaller group +8-4= 44 answer!different symbol = subtractleft over symbol is positive give to answer