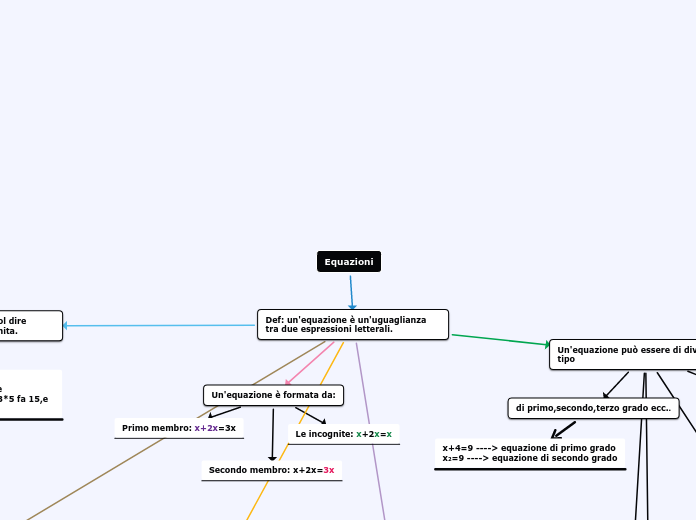
Equazioni
Def: un'equazione è un'uguaglianza tra due espressioni letterali.
Risolvere un'equazione vuol dire trovare il valore dell'incognita.
ES: 3x=15 In questo caso la soluzione dell'equazione è 5,perchè 3*5 fa 15,e quindi X=5.
L'obbiettivo,quando si risolve un'equazione è quello di trasformala in forma normale,ovvero con tutte le incognite nel primo membro,e i numeri interi nel secondo.
Un'equazione può essere di diverso tipo
di primo,secondo,terzo grado ecc..
x+4=9 ----> equazione di primo grado x2=9 ----> equazione di secondo grado
Intera o frazionaria
1/4 x+3=2x-1 --->equazione intera,le frazioni non hanno un'incognita come denominatore.
2/x -5=1/3 --->equazione frazionaria,il denominatore del primo membro è un'incognita.
Determinata,quando l'incognita può assumere il valore di un solo numero.
x=5 ,in questo caso la soluzione è 5 e x non può assumere nessun'altro valore,altrimenti l'uguaglianza non sarebbe vera.
Indeterminata,o identità,quando l'incognita può assumere il valore di tutti i numeri,l'uguaglianza sarà sempre vera.
0x=0 ,questa equazione è un'identità perchè qualunque valore assuma x,l'uguaglianza rimane vera.Infatti tutti i numeri moltiplicati per 0 danno 0.
Impossibile,quando l'uguaglianza non è mai vera,qualunque valore assuma l'incognita.
0x=2 , questa equazione è impossibile.Non esiste nessun numero che moltipplicato per 0 dà 2.
Un'equazione è formata da:
Primo membro: x+2x=3x
Secondo membro: x+2x=3x
Le incognite: x+2x=x
Primo principio di equivalenza Def: addizionando o sottraendo ai due membri di un'equazione uno stesso numero o una stessa espressione algebrica contenente l'incognita,si ottiene un'equazione equivalente a quella data.
Es: 2x+5-1/2 =6x+5x 2x+5-1/2 -5=6x+5x-5 2x-1/2 =6x+x In questo caso,il primo principio di equivalenza ci è servito per semplificare l'equazione,ma per andare avanti e raggiungere la forma normale dell'equazione ci serve un'altro principio,derivante dal primo.
Il principio del trasporto Questo principio dice che,puoi spostare una quantità dal primo al secondo membro,ricordandoti però,di cambiare il segno a ciò che stai trasportando.
Proviamo ora a continuare l'espressione di prima. 2x-6x-x=+1/2 -5x=1/2
Secondo principio di equivalenza Def:moltiplicando o dividendo i due membri di un'equazione per uno stesso numero diverso da zero,si ottiene un'equazione equivalente a quella data.
Es: 3/4x+1/2=-2/3x+1 (9x+6)/12=(-8x+12)/12 12* (9x+6)/12=(-8x+12)/12 *12 9x+6=-8x+12 9x+8x=-6+12 17x=6 17x/17=6/17 x=6/17 S={6/17}
Verifica di un'equazione Per fare la verifica di un'equazione,per controllare se la soluzione è giusta,basta riprende l'equazione di partenza e sostituire fin da subito l'incognita con il suo valore.
3/4*6/17+1/2=-2/3*6/17+1 9/34+1/2=-4/17 +1 9+17/34=-4+17/17 26/34=13/17 Questa uguaglianza è vera,perchè se semplifichiamo 26/34 viene 13/17