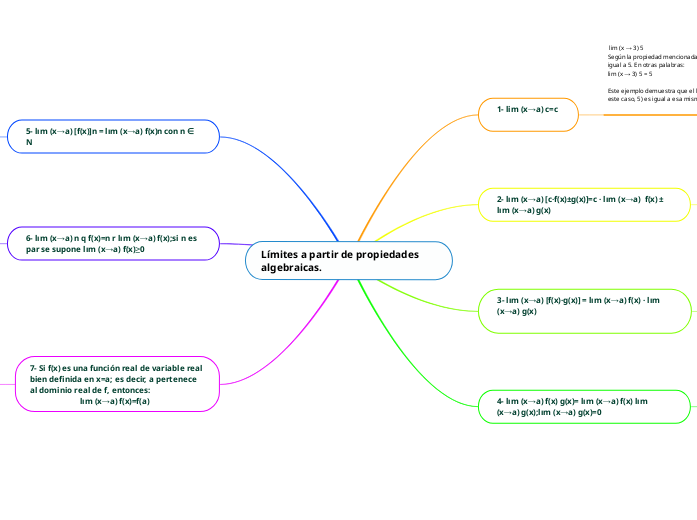
Límites a partir de propiedades algebraicas.
1- lim (x→a) c=c
lim (x → 3) 5
Según la propiedad mencionada, el límite de la constante 5 es igual a 5. En otras palabras:
lim (x → 3) 5 = 5
Este ejemplo demuestra que el límite de una constante (en este caso, 5) es igual a esa misma constante.
2- lım (x→a) [c·f(x)±g(x)]=c · lım (x→a) f(x) ± lım (x→a) g(x)
lim (x → 2) [3 * x^2 + 5x]
lim (x → 2) [3 * x^2] + lim (x → 2) [5x]
lim (x → 2) [3 * x^2] = 3 * lim (x → 2) [x^2]
lim (x → 2) [5x] = 5 * lim (x → 2) [x]
lim (x → 2) [3 * x^2] = 3 * (2^2) = 3 * 4 = 12
lim (x → 2) [5x] = 5 * 2 = 10
lim (x → 2) [3 * x^2 + 5x] = 12 + 10 = 22
3- lım (x→a) [f(x)·g(x)] = lım (x→a) f(x) · lım (x→a) g(x)
lim (x → 3) [x^2 * (2x - 1)]
lim (x → 3) [x^2] * lim (x → 3) [2x - 1]
lim (x → 3) [x^2] = 3^2 = 9
lim (x → 3) [2x - 1] = 2 * 3 - 1 = 6 - 1 = 5
lim (x → 3) [x^2 * (2x - 1)] = 9 * 5 = 45
Por lo tanto, el límite de la expresión original cuando x se acerca a 3 es igual a 45.
4- lım (x→a) f(x) g(x)= lım (x→a) f(x) lım (x→a) g(x);lım (x→a) g(x)=0
lim (x → 2) [x^2 * (3x - 2)]
lim (x → 2) [x^2] = 2^2 = 4
lim (x → 2) [3x - 2] = 3 * 2 - 2 = 6 - 2 = 4
lim (x → 2) [x^2 * (3x - 2)] = 4 * 4 = 16
Por lo tanto, el límite de la expresión original cuando x se acerca a 2 es igual a 16.
5- lım (x→a) [f(x)]n = lım (x→a) f(x)n con n ∈ N
lim (x → 1) [x^2]^3
lim (x → 1) [x^2] = (1^2) = 1
[lim (x → 1) x^2]^3 = (1)^3 = 1^3 = 1
Por lo tanto, el límite de la expresión original cuando x se acerca a 1 es igual a 1.
6- lım (x→a) n q f(x)=n r lım (x→a) f(x);si n es par se supone lım (x→a) f(x)≥0
lim (x → 2) [3 * x^2]^4
lim (x → 2) [3 * x^2] = 3 * (2^2) = 3 * 4 = 12
3^4 * [lim (x → 2) x^2]^4 = 81 * (12)^4
12^4 = 20,736
81 * 20,736 = 1,679,616
Por lo tanto, el límite de la expresión original cuando x se acerca a 2 es igual a 1,679,616.
7- Si f(x) es una función real de variable real bien definida en x=a; es decir, a pertenece al dominio real de f, entonces:
lım (x→a) f(x)=f(a)
Considera la función f(x) = x^2. Esta función es una función real de variable real en cualquier punto del dominio real. Ahora, vamos a demostrar la propiedad:
lim (x → 2) x^2
lim (x → 2) x^2 = 2^2 = 4
f(2) = 2^2 = 4
lim (x → 2) x^2 = f(2)
Esta propiedad es válida para cualquier función real de variable real que esté bien definida en un punto a dentro de su dominio real.