FUNCIONES, MODELOS Y LIMITES DE UNA FUNCION
DEFINICIÓN DE UNA FUNCIÓN
RELACIÓN DE LOS ELEMENTO DE A CON LOS ELEMENTOS DE B TAL QUE CADA ELEMENTO DE A LE CORRESPONDE UN ÚNICO ELEMENTO B.
REPRESENTACION DE UNA FUNCION
LA REPRESENTACIÓN DE UNA FUNCIÓN PUEDE HACERSE DE DIVERSAS FORMAS:
DOMINIO DE UNA FUNCION:
EL DOMINIO Y RANGO DE UNA FUNCIÓN DADA DE FORMA ANALÍTICA, SERÁN LAS EXTENSIONES DE LA ECUACIÓN IMPLICADA, A MENOS QUE SE INDIQUE OTRA COSA. AUN ASÍ EL DOMINIO DE LA FUNCIÓN DEBERÁN SER AL MENOS UNA PORCIÓN DE LAS EXTENSIONES DE LA CURVA.
y = f (x)
CLASIFICACIÓN DE FUNCIONES
LAS FUNCIONES SE CLASIFICAN TAMBIÉN SEGÚN EL TIPO DE EXPRESIÓN QUE APARECE EN LA REGLA DE CORRESPONDENCIA. ES ESTA LA QUE LE DA EL NOMBRE A LA FUNCIÓN.
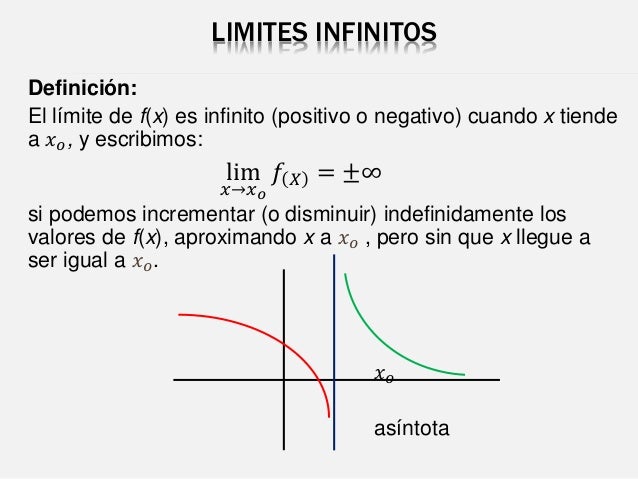
ASÍNTOTA HORIZONTAL
LIMITE AL INFINITO
LIMITES DE FUNCIONES
SI EL VALOR DE UNA FUNCION SE APROXIMA AL MISMO NUMERO L CONFORME X SE ACERCA HACIA a DESDE AMBAS DIRECCIONES, ENTONCES EL LIMITE ES IGUAL A L.
GRAFICA
ANALITICA
SAGITAL



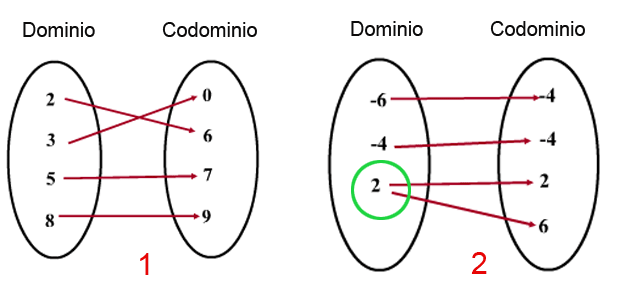
ESTA CONFORMADO POR UN DOMINIO Y POR UN CONTRADOMINIO, FORMANDO ASI UN RANGO.

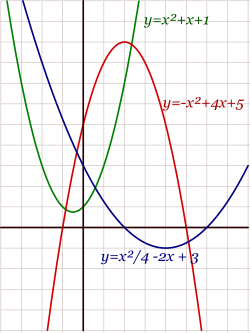
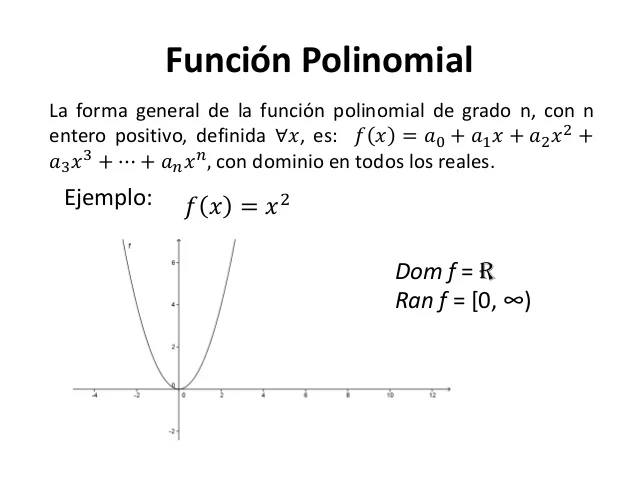
CUADRATICA
lim f (x) = L