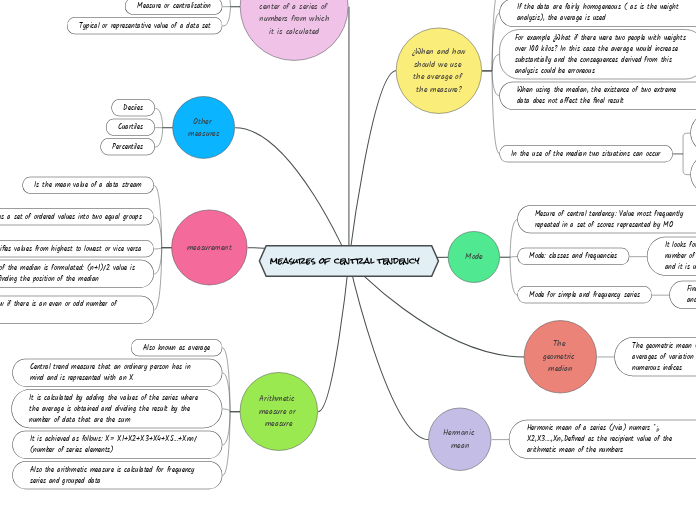
measures of central tendency

The answer will have to do with the data collected

If the data are fairly homogeneous ( as is the weight analysis), the average is used

For example ¿What if there were two people with weights over 100 kilos? In this case the average would increase substantially and the consequences derived from this analysis could be erroneous

When using the median, the existence of two extreme data does not affect the final result

In the use of the median two situations can occur

If the sample size is an odd number, the median would be the one that separates in equal parts to the series, to obtain this data the formula is the following: (n+1)/2

If the sample size is an even number, then the median will be the average value between the two data dividing the series

Mesure of central tendency: Value most frequently repeated in a set of scores represented by MO

Mode: classes and frequencies

It looks for the value that is repeated and the greatest number of times, only that they are grouped in classes and it is used this means that continues the mode

Mode for simple and frequency series

Find the value that most times are repeated in the series and without making any calculation or formula

The geometric mean (Mg) is used in the calculation of averages of variation rates and in the elavoration of the numerous indices

Hermonic mean of a series (/via) numers *¡, X2,X3....,Xn,.Defined as the recipient value of the arithmetic mean of the numbers

Average

Measure or centralisation

Typical or representative value of a data set

Deciies

Cuartiles

Percentiles

Is the mean value of a data stream

Divides a set of ordered values into two equal groups

Half of the numbers will have values that are lower than the median and the other half will reach higher values and is represented by the letters MD

Classifies values from highest to lowest or vice versa

The position of the median is formulated: (n+1)/2 value is obtained by finding the position of the median

Count to know if there is an even or odd number of values

Odd: median is central value

torque: average of core values

Also known as average

Central trend measure that an ordinary person has in mind and is represented with an X

It is calculated by adding the values of the series where the average is obtained and dividing the result by the number of data that are the sum

It is achieved as follows: X= X1+X2+X3+X4+X5...+Xnn/ (number of series elements)

Also the arithmetic measure is calculated for frequency series and grouped data