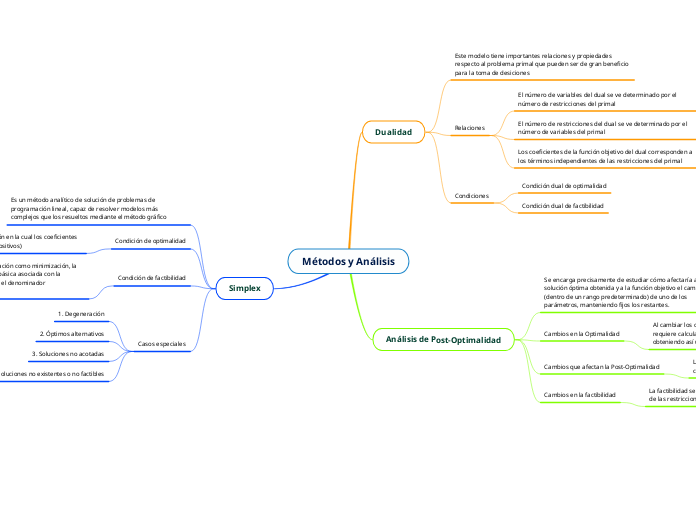
Métodos y Análisis
Dualidad
Este modelo tiene importantes relaciones y propiedades respecto al problema primal que pueden ser de gran beneficio para la toma de desiciones
Relaciones
El número de variables del dual se ve determinado por el número de restricciones del primal
El número de restricciones del dual se ve determinado por el número de variables del primal
Los coeficientes de la función objetivo del dual corresponden a los términos independientes de las restricciones del primal
Condiciones
Condición dual de optimalidad
Condición dual de factibilidad
Análisis de Post-Optimalidad
Se encarga precisamente de estudiar cómo afectaría a la solución óptima obtenida y a la función objetivo el cambio (dentro de un rango predeterminado) de uno de los parámetros, manteniendo fijos los restantes.
Cambios en la Optimalidad
Al cambiar los coeficiientes, cambia la optimalidad y se requiere calcular nuevos coeficientes para la función objetivo, obteniendo así un nuevo valor de Z
Cambios que afectan la Post-Optimalidad
La Post-Optimalidad se ve afectada por los cambios en los coeficientes objetivos y la adición de una nueva variable
Cambios en la factibilidad
La factibilidad se ve afectada cuando cambia el lado derecho de las restricciones o se agrega una restricción al modelo
Simplex
Es un método analítico de solución de problemas de programación lineal, capaz de resolver modelos más complejos que los resueltos mediante el método gráfico
Condición de optimalidad
El óptimo se alcanza en la iteración en la cual los coeficientes en la fila z son no negativos (no positivos)
Condición de factibilidad
Tanto en problemas de maximización como minimización, la variable de salida es la variable básica asociada con la relación mínima no negativa con el denominador estrictamente positivo
Casos especiales
1. Degeneración
2. Óptimos alternativos
3. Soluciones no acotadas
4. Soluciones no existentes o no factibles