razones trigonométricas para triángulos rectángulos y sus aplicaciones
trigonometria y sus aplicaciones
fueron una de las herramientas que usaron los pueblos antiguos para resolver problemas que se presentaban en su
cotidianidad. El origen de la trigonometría se remonta a hace más de 4000 años.
unas de sus aplicaciones más destacadas se muestran en la navegación, la geografía, la astronomía, la arquitectura y en todos los campos de la ingeniería. La utilización de la trigonometría en las ciencias y en la vida cotidiana se debe a que a través de esta se obtienen medidas precisas
Existen diversas aplicaciones de la trigonometría en la ciencia y en la vida cotidiana. Uno de los ejemplos más notables de ello es en la matemática, ya que interviene en todos sus campos
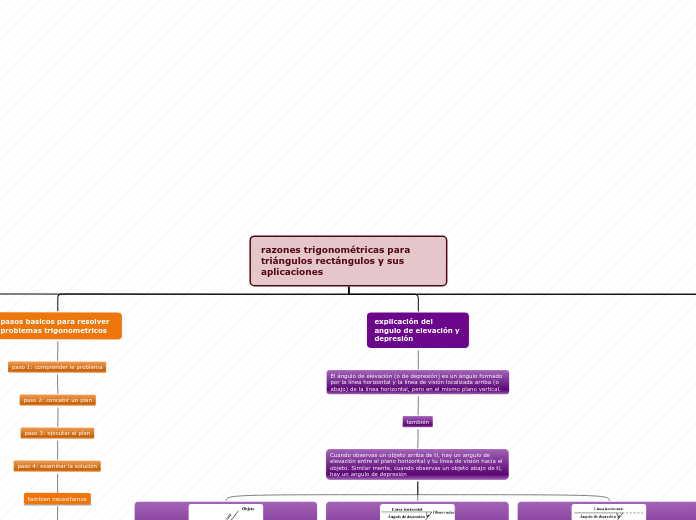
pasos basicos para resolver problemas trigonometricos
paso 1: comprender le problema
paso 2: concebir un plan
paso 3: ejecutar el plan
paso 4: examinar la solución
tambien necesitamos
Las identidades trigonométricas

explicación del angulo de elevación y depresión
El ángulo de elevación (o de depresión) es un ángulo formado por la línea horizontal y la línea de visión localizada arriba (o abajo) de la línea horizontal, pero en el mismo plano vertical.
también
Cuando observas un objeto arriba de tí, hay un angulo de elevación entre el plano horizontal y tu línea de visión hacia el objeto. Similar mente, cuando observas un objeto abajo de ti, hay un angulo de depresión

El término ángulo de elevación denota al ángulo desde la horizontal hacia arriba a un objeto. Una línea de vista para el observador estaría sobre la horizontal.

El término ángulo de depresión denota al ángulo desde la horizontal hacia abajo a un objeto. Una línea de vista para el observador estaría debajo de la horizontal

Dese cuenta que el ángulo de elevación y el ángulo de depresión son congruentes
como se resuelven solución de triángulos rectángulos
Resolver un triangulo es hallar la longitud de sus lados, la medida de sus ángulos agudos y el área, es necesario conocer dos lados del triángulo, o bien un lado y un ángulo agudos internos, con base en estas condiciones se presentan cuatro casos en la resolución de triángulosj
que son
1 Se conocen la hipotenusa y un cateto.
2 Se conocen los dos catetos.
3 Se conocen la hipotenusa y un ángulo agudo.
4 Se conocen un cateto y un ángulo agudo