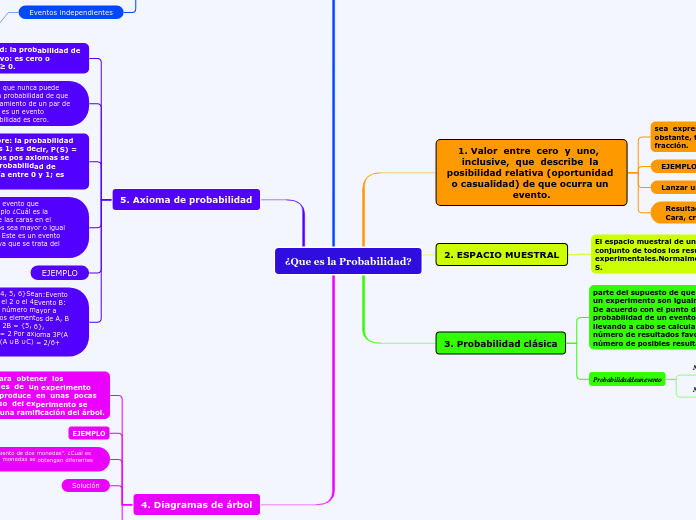
¿Que es la Probabilidad?
1. Valor entre cero y uno, inclusive, que describe la posibilidad relativa (oportunidad o casualidad) de que ocurra un evento.
sea expresada en forma decimal, no obstante, también se da en forma de fracción.
EJEMPLO
Lanzar una moneda
Resultado experimentalLanzar una moneda Cara, cruz
2. ESPACIO MUESTRAL
El espacio muestral de un experimento es el conjunto de todos los resultados experimentales.Normalmente se denota por S.
3. Probabilidad clásica
parte del supuesto de que los resultados de un experimento son igualmente posibles. De acuerdo con el punto de vista clásico, la probabilidad de un evento que se está llevando a cabo se calcula dividiendo el número de resultados favorables entre el número de posibles resultados:
𝑃𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑑𝑎𝑑𝑑𝑒𝑢𝑛𝑒𝑣𝑒𝑛𝑡𝑜
𝑁ú𝑚𝑒𝑟𝑜𝑑𝑒𝑟𝑒𝑠𝑢𝑙𝑡𝑎𝑑𝑜𝑠𝑓𝑎𝑣𝑜𝑟𝑎𝑏𝑙𝑒
𝑁ú𝑚𝑒𝑟𝑜𝑡𝑜𝑡𝑎𝑙𝑑𝑒𝑝𝑜𝑠𝑖𝑏𝑙𝑒𝑠𝑟𝑒𝑠𝑢𝑙𝑡𝑎𝑑𝑜𝑠
6. Tipos de eventos
Eventos mutuamente excluyentes.
dos eventos A y B son mutuamente excluyentes si A y B no contienen puntos muestrales en común, es decir su intersección es el conjunto vacío: 𝐴∩𝐵=∅
Eventos solapados
Dos eventos A y B, son solapados o unidos, si tienen puntos muéstrales en común. Al subconjunto que contiene los puntos comunes de A y B se le llama intersección de A y B y se denota por 𝐴∩𝐵. Por lo tanto la probabilidad de la unión de los eventos la obtendremos mediante: 𝑃(𝐴𝑜𝐵)=𝑃(𝐴∪𝐵)=𝑃(𝐴)+𝑃(𝐵)−𝑃(𝐴∩𝐵)
Eventos complementarios
Son dos resultados de un evento, siendo éstos los dos únicos resultados posibles.
Eventos independientes
Se dice que dos o más eventos son independientes si no tienen relación alguna entre sí o la aparición de cualquiera de ellos no afecta en absoluto la probabilidad de aparición del otro u otros.
5. Axioma de probabilidad
Axioma 1 de positividad: la probabilidad de un evento es no negativo: es cero o positivo; es decir P(E) ≥ 0.
La P(E) = 0 significa un evento que nunca puede ocurrir, por ejemplo ¿Cuál es la probabilidad de que la suma de las caras en el lanzamiento de un par de dados sea mayor que 12? Este es un evento imposible por lo tanto la probabilidad es cero.
Axioma 2 de certidumbre: la probabilidad del espacio muestral es 1; es decir, P(S) = 1. Entonces tomando los pos axiomas se puede afirmar que la probabilidad de cualquier evento E varía entre 0 y 1; es decir 0≤P(E)≤1.
La P(E) = 1 significa que es un evento que ciertamente ocurrirá: por ejemplo ¿Cuál es la probabilidad de que la suma de las caras en el lanzamiento de un par de dados sea mayor o igual que 2 y menor o igual que 12? Este es un evento seguro y la probabilidad es 1, ya que se trata del espacio muestral completo.
EJEMPLO
Se lanza un dado, S={1, 2, 3, 4, 5, 6}Sean:Evento A: que al lanzar un dado salga el 2 o el 4Evento B: que al lanzar un dado salga un número mayor a 4Evento C: que salga el 1 o 3Los elementos de A, B y C sonA = {2, 4}, N(A) = 2B = {5, 6}, N(B) = 2C = {1, 3}, N(C) = 2 Por axioma 3P(A ∪B ∪C) = P(A) + P(B) + P(C)P(A ∪B ∪C) = 2/6+ 2/6+ 2/6 = 6/6 = 1
4. Diagramas de árbol
Es un método para obtener los resultados posibles de un experimento cuando éste se produce en unas pocas etapas. Cada paso del experimento se representa como una ramificación del árbol.
EJEMPLO
Dado el experimento “lanzamiento de dos monedas”. ¿Cuál es la probabilidad que en ambas monedas se obtengan diferentes resultados?
Solución
Para poder encontrar la probabilidad, primero debemos encontrar todos los casos posibles del experimento,
CARA
CARA
CARA CARA
CRUZ
CARA CRUZ
CRUZ
CARA
CRUZ CARA
CRUZ
CRUZ CRUZ
Del diagrama obtenemos que S={(cara,cara), (cara, cruz), (cruz, cara), (cruz, cruz)}.Observando todos los casos posibles tenemos que únicamente hay dos casos en donde los resultados son diferentes que son (cara, cruz)y(cruz, cara).Así,Casos favorables: 2Casos posibles: 4