TRIGONOMETRIA
La trigonometría es una rama de la matemática cuyo significado etimológico es 'la medición de los triángulos'. La trigonometría se aplica a otras ramas de la geometría o la geometría analítica en particular geometría plana o geometría del espacio.
Medición de triángulos
Se usan las leyes del seno y del coseno y de la tangente.
Ley del seno

Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos.
Ley coseno

En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto del producto de ambos por el coseno del ángulo que forman.
Ley de tangente

Si A y B son ángulos de un triángulo y sus lados correspondientes son a y b.
Funciones trigonométricas
Las funciones trigonométricas son las funciones determinadas con el objetivo de extender la definición de las razones trigonométricas a todos los números reales y complejos.
se dividen en directos y recíprocos
Directos
SEN Ø = CAT. OPUESTO . HIPOTENUSA COS Ø = CAT.ADYACENTE . HIPOTENUSA TAN Ø = CAT. OPUESTO CAT. ADYACENTE
Recíprocos
CSC Ø = 1 = CAT. OPUESTO
SEN Ø HIPOTENUSA
SEC Ø = 1 = CAT. ADYACENTE
COS Ø HIPOTENUSA
COT Ø = 1 = CAT. OPUESTO
TAN Ø CAT. ADYACENTE
Todo signo de una función trigonométrica depende del cuadrante donde se encuentre su ángulo relacionado.
Se dividen principalmente en:
Ángulo compuesto
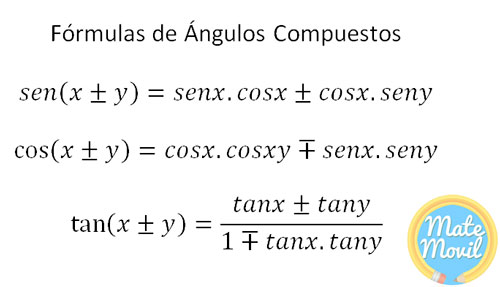
Podemos hallar otras identidades tales como la de la suma de ángulos o la diferencia de ángulos.

Ángulo doble

Ángulo medio

