Чотирикутники

Még több ilyen

Середньовіччя V-XV ст.

Szerző: Максим Полянський

Інформація 2 клас

Szerző: Fedorova Nastya

Тематика веб-квестів з геометрії 7 класу

Szerző: Mariana Yasinska

Алотропія

Szerző: Прокоф'єва Марія

Чотирикутники

Чотирикутник — фігура, яка складається з чотирьох точок (жодні три з них не лежать на одній прямій) і чотирьох відрізків, які з'єднують послідовно ці точки і не перетинаються.

Задачі про чотирикутники

Після того як ви пройшли увесь матеріал перевірте свої знання. Спробуйте вирішити наступні задачі.

Рівнобедрена трапеція описана навколо кола. Бічна сторона трапеції поділяється точкою дотику на відрізки 12см і 48 см. Знайти площу трапеції.

Паралелограм розрізали на три рівнобедрені трикутники. Знайдіть кути паралелограма.

Периметр ромба 40 см. Одна з діагоналей утворює із стороною ромба кут 15 градусів. Знайти площу ромба.

Чотирикутники навколо нас

Чотирикутники майже скрізь оточують нас

Види чотирикутників

В данному блоці ви дізнаєтесь про види чотирикутників а саме:

До паралелограмів відносяться:

- Квадрат

- Ромб

- Прямокутник

Довільні чотирикутники

Чотирикутник — це частина площини, обмежена простою замкненою ламаною, яка містить чотири (4) ланки. Вона складається з чотирьох (4) вершин (точок) і чотирьох сторін (відрізків), що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій

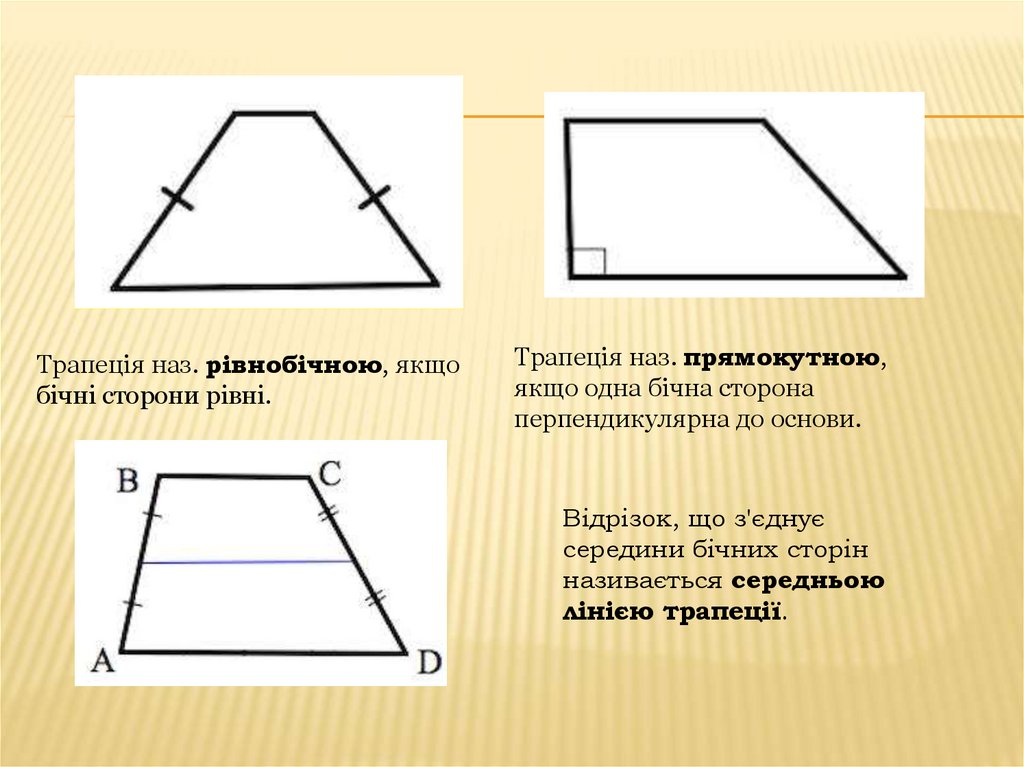
Трапеції бувають:

• Рівнобічні
• Різносторонні
• Прямокутні

Властивості

Уважно прочитайте властивості та запам'ятайте їх.

• Діагоналі прямокутника рівні.
• Діагоналі прямокутника перетинаються і точкою перетину діляться навпіл.
• Діагоналі прямокутника ділять його на два рівні трикутники.
• Висоти прямокутника є одночасно і його сторонами.
• Навколо будь-якого прямокутника можна описати коло, причому діагональ прямокутника дорівнює діаметру даного кола.
• Квадрат діагоналі прямокутника дорівнює сумі квадратів двох його не протилежних сторін.

Прямокутник є плоскою геометричною фігурою, його аналогом у тривимірному просторі є прямокутний паралелепіпед.

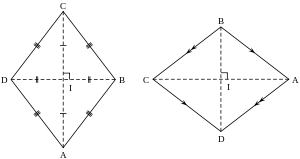
Кожен ромб має дві діагоналі, що з'єднують пари протилежних вершин, і має дві пари паралельних сторін. Звідси випливає, що ромб має такі властивості:

• Це паралелограм, діагоналі якого розділяють внутрішній кут.
• Протилежні кути ромба рівні.
• Діагоналі ромба перетинаються під прямим кутом, точка перетину є серединою кожної діагоналі.
• Діагоналі ромба є бісектрисами кутів, з яких вони проведені.
• Сторони ромба попарно паралельні.
• Точка перетину діагоналей називається центром симетрії ромба.
• В будь-який ромб можна вписати коло.
• Центром кола, вписаного в ромб, є точка перетину його діагоналей.
• Сума квадратів діагоналей дорівнює квадрату сторони, помноженому на чотири: AC² + BD² = 4AB²

Однією з основних властивостей є те, що ромб - це паралелограм, внаслідок чого ромб має усі ті властивості, що й паралелограм. Наприклад,

• протилежні сторони паралельні;
• прилеглі кути є суміжними;
• дві діагоналі поділяють одна одну навпіл;
• будь-яка пряма, що проходить через центр, поділяє площу навпіл;
• сума квадратів сторін дорівнює сумі квадратів діагоналей (правило паралелограма).

Отож, якщо позначити сторону як a, а діагоналі як d₁ і d₂, то для кожного ромба

Не кожен паралелограм є ромбом, але кожен паралелограм, у якого діагоналі є перпендикулярними, є ромбом. В загальному випадку будь-який чотирикутник з перпендикулярними діагоналями, одна з яких є лінією симетрії, - це дельтоїд.

1. У паралелограма протилежні сторони рівні.
2. У паралелограма протилежні кути рівні.
3. Діагоналі паралелограма у точці перетину діляться навпіл.
4. У паралелограма сума кутів, які прилягають до однієї сторони дорівнює 180 градусів.

Ознаки

Проаналізуйте наступні ознаки чотирикутників та знайдіть спільні.

Прямокутник

•  Якщо три кути чотирикутника прямі, то такий чотирикутник є прямокутником.

•  Якщо один кут паралелограма прямий, то такий паралелограм є прямокутником.

•  Якщо діагоналі паралелограма рівні, то такий паралелограм є прямокутником.

Паралелограм ABCD буде ромбом, якщо виконується хоча б одна з таких умов:

• Дві його суміжні сторони рівні (звідси випливає, що всі сторони рівні): АВ = ВС = СD = AD
• Його діагоналі перетинаються під прямим кутом: AC┴BD
• Одна із діагоналей (бісектриса) ділить кути навпіл:
• ∠BAC = ∠CAD або ∠BDA = ∠BDC
• Якщо всі висоти рівні: BN = DL = BM = DK
• Якщо діагоналі ділять паралелограм на чотири рівні прямокутні трикутники:
• Δ ABO = Δ BCO = Δ CDO = Δ ADO
• Якщо в паралелограм можна вписати коло.

Паралелограм

1. Якщо у чотирикутнику дві протилежні сторони паралельні і рівні, то такий чотирикутник паралелограм.
2. Якщо у чотирикутнику діагоналі точкою перетину діляться пополам, то такий чотирикутник- паралелограм.
3. Якщо у чотирикутнику кожні два протилежні кути рівні, то такий чотирикутник - паралелограм.
4. Якщо у чотирикутнику кожні дві протилежні сторони рівні, то такий чотирикутник- паралелограм.

Площі чотирикутників

Перегляньте відеоролики щоб досконально розібратись як знаходити площу будь-якого чотирикутника.

Паралелограми

Ромб

Трапеції