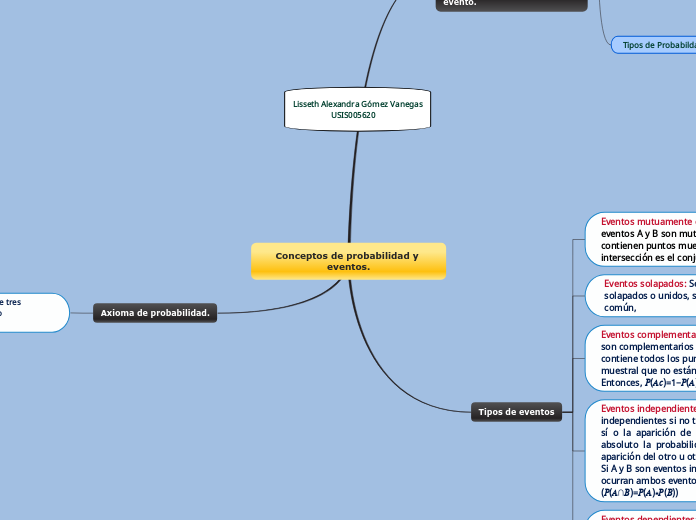
Conceptos de probabilidad y eventos.

Még több ilyen

Calidad en Trabajos Académicos

Szerző: Lluis Codina

LOS ELEMENTOS DE LA EVALUACIÓN

Szerző: Elizabeth Pérez Paiz

NIA 530 MUESTREO DE AUDITORIA

Szerző: JAIME SALVADOR ARAGON ARGUETA

NIF B4. Estado de variaciones al capital contable

Szerző: Andrés Emiliano Estrada Mata

Lisseth Alexandra Gómez Vanegas USIS005620

Conceptos de probabilidad y eventos.

Axioma de probabilidad.

El cálculo de probabilidades tiene tres axiomas o postulados del evento probabilístico

Axioma 3 de las uniones: la probabilidad de un evento compuesto E es igual a la suma de las probabilidades de los eventos simples de los cuales E es compuesto; es decir Ei es un evento compuesto de los eventos simples e1, e2, e3,..., ek; entonces P(E) = P(e1) + P(e2) + P(e3)+...+ P(ek).

Axioma 2 de certidumbre: la probabilidad del espacio muestral es 1; es decir, P(S) = 1

Axioma 1 de positividad: la probabilidad de un evento es no negativo: es cero o positivo; es decir P(E) ≥ 0.

Tipos de eventos

Eventos dependientes: Dos o más eventos son dependientes cuando la probabilidad de ocurrencia o no ocurrencia de uno de esos eventos, afecta la probabilidad de otros eventos, en otras pruebas. Si A y B son dependientes entonces, 𝑃(𝐴∩𝐵)=𝑃(𝐴)∗𝑃(𝐵/𝐴) 𝑃(𝐵/𝐴) se entenderá como la probabilidad de que suceda el evento B dado que ya sucedió el evento A.

Eventos independientes: Se dice que dos o más eventos son independientes si no tienen relación alguna entre sí o la aparición de cualquiera de ellos no afecta en absoluto la probabilidad de aparición del otro u otros. Si A y B son eventos independientes la probabilidad de que ocurran ambos eventos se calculará mediante, (𝑃(𝐴∩𝐵)=𝑃(𝐴)∗𝑃(𝐵))

Eventos complementarios: Se dice que los eventos 𝐴 y 𝐴𝐶 son complementarios si 𝐴𝐶 es un subconjunto que contiene todos los puntos muestrales del espacio muestral que no están en 𝐴. Entonces, 𝑃(𝐴𝑐)=1−𝑃(𝐴)

Eventos solapados: Se dice que dos eventos A y B, son solapados o unidos, si tienen puntos muéstrales en común,

Eventos mutuamente excluyentes: Decimos que dos eventos A y B son mutuamente excluyentes si A y B no contienen puntos muestrales en común, es decir su intersección es el conjunto vacío: 𝐴∩𝐵 =∅

Probabolidad: Valor entre cero y uno, inclusive, que describe la posibilidad relativa (oportunidad o casualidad) de que ocurra un evento.

Tipos de Probabildades

El diagrama de árbol es un método para obtener los resultados posibles de un experimento cuando éste se produce en unas pocas etapas. Cada paso del experimento se representa como una ramificación del árbol.

ejemplo no tan exacto

La probabilidad clásica parte del supuesto de que los resultados de un experimento son igualmente posibles.

𝑃𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑑𝑎𝑑 𝑑𝑒 𝑢𝑛 𝑒𝑣𝑒𝑛𝑡𝑜 = 𝑁ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑟𝑒𝑠𝑢𝑙𝑡𝑎𝑑𝑜𝑠 𝑓𝑎𝑣𝑜𝑟𝑎𝑏𝑙𝑒𝑠 𝑁ú𝑚𝑒𝑟𝑜 𝑡𝑜𝑡𝑎𝑙 𝑑𝑒 𝑝𝑜𝑠𝑖𝑏𝑙𝑒𝑠 𝑟𝑒𝑠𝑢𝑙𝑡𝑎𝑑𝑜𝑠

Partes de la probabilidad

EVENTO Conjunto de uno o más resultados de un experimento.

RESULTADO: consecuencia obtenida al realizar un experimento.

EXPERIMENTO: Proceso que induce a que ocurra una y sólo una de varias posibles observaciones.