a JUAREZ SERVIN AYLIN DANAE 3 éve
293
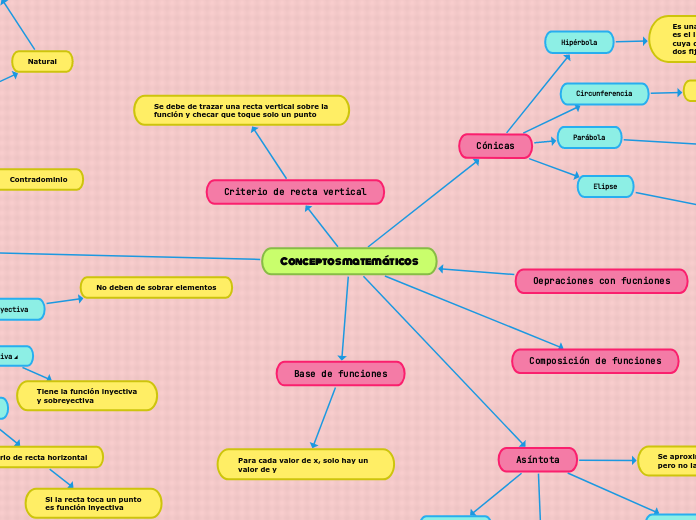
Conceptos matemáticos
a JUAREZ SERVIN AYLIN DANAE 3 éve
293

Még több ilyen


Szerző: Juan Jose Hernandez

Szerző: James Mosquera Renteria

Szerző: Carol Diaz

Szerző: leidy guadalupe flores bazaldua
y= 3x+5
Si la recta toca un punto es función inyectiva
Máximo dominio
Subtopic
Natural