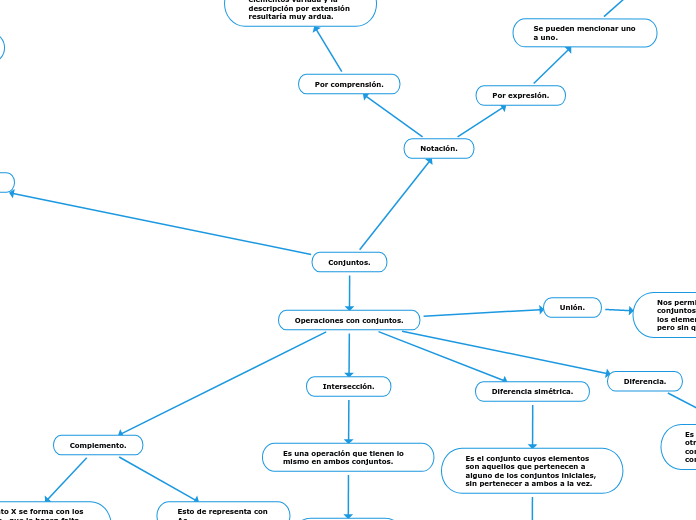
Conjuntos.

Még több ilyen

SOFTWARE PARA INGENIERÍA QUÍMICA

Szerző: Guadalupe Rivera

El término Revolución rusa agrupa todos los sucesos que condujeron al derrocamiento del régimen zarista imperial y a la instauración preparada de otro, leninista republicano, entre febrero y octubre de 1917

Szerző: valery Fernandez

NUMEROS REALES (R)

Szerző: JUAN SEBASTIAN NIETO LOPEZ

FRACCIONES ALGEBRAICAS

Szerző: Ireth Izquierdo Davila

Conjuntos.

Tipos de conjuntos.

Conjuntos disjuntos.

Conjuntos que no tienen ningún elemento en común, conjuntos vacíos

Números impares del 1 a el 7

B = {1, 3, 5, 7}

Conjuntos sin nada en comú.

Números pares del 2 a el 8

A = {2, 4, 6, 8}

Conjunto vacío.

Conjunto que carece de elementos.

A = f

A = {}

Subconjuntos.

Conjunto cuyos elementos pertenecen a otro conjunto determinado.

B = {1, 2, 3, 4, 5}

A es subconjunto de B

A = {1, 2, 3}

Igualdad de conjuntos.

Dos conjuntos son iguales en el caso de que contengan los mismos elementos.

A ={ números pares del 2 al 14}

B= {2, 4, 6, 8, 10, 12, 14}

A=B

Operaciones con conjuntos.

Unión.

Nos permite unir dos o mas conjuntos que contendrá a todos los elementos que queremos unir pero sin que se repitan.

N = {g, b, e, l}

M u N = {a, c, b, e, l, g}

M = {a, c, b}

Diferencia.

Es una operación que da como resultado otro conjunto con los elementos del primer conjunto sin los elementos del segundo conjunto.

B = {f, r, j, u, o}

A-B = {d, g, t}

A = {d, f, g , r, t}

Diferencia simétrica.

Es el conjunto cuyos elementos son aquellos que pertenecen a alguno de los conjuntos iniciales, sin pertenecer a ambos a la vez.

R = {1, 6, 5}

{2, 9, 3}

D = {2, 6, 9, 5, 3}

Complemento.

Esto de representa con Ac.

Un conjunto X se forma con los elementos que le hacen falta al conjunto X para ser igual al conjunto universal.

U = {1, 3, 5, 7, 9, 11}

Ac= {9, 11}

A = {1, 3, 5, 7}

Intersección.

Es una operación que tienen lo mismo en ambos conjuntos.

Notación.

Por expresión.

Se pueden mencionar uno a uno.

F es el conjunto de los colores primarios

F = {Amarillo, azul, rojo}

Por comprensión.

Tienen una cantidad de elementos variada y la descripción por extensión resultaría muy ardua.

Ejemplo:

C es el conjunto conformado por todos los países

C = {Colombia/Colombia es un país}