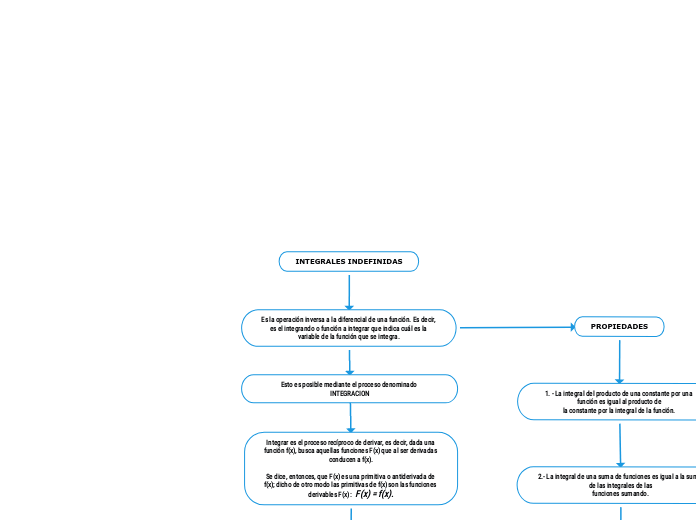
INTEGRALES INDEFINIDAS

Még több ilyen

El hombre y la sociedad.

Szerző: leisly aguilar lopez

Materia dispersa

Szerző: A Fidalgo

integral indefinida

Szerző: Itziar Echeandía

GESTÁLTICO VISOMOTOR DE BENDER

Szerző: LUZ LAYNES

INTEGRALES INDEFINIDAS

Es la operación inversa a la diferencial de una función. Es decir, es el integrando o función a integrar que indica cuál es la variable de la función que se integra.

PROPIEDADES

1. - La integral del producto de una constante por una función es igual al producto de la constante por la integral de la función.

2.- La integral de una suma de funciones es igual a la suma de las integrales de las funciones sumando.

3.- la integral de una diferencia de funciones es igual a la diferencia de las integrales de las funciones minuendo y sustraendo.

4.- Como consecuencia de las dos propiedades anteriores: La integral de una suma algebraica de funciones es igual a la suma algebraica de las integrales de todas y cada una de las funciones sumandos.

∫(x − x + )dx = ∫x dx − ∫x dx + ∫dx = x3/3 - x2/2 | x + c

∫[ƒ(x) - g(x)] dx = ∫ƒ(x) dx - ∫g(x) dx

∫[ƒ(x) + g(x)] dx = ∫ƒ(x) dx + ∫g(x) dx

∫c ⋅ f (x) dx = c ⋅∫ f (x)dx

Esto es posible mediante el proceso denominado INTEGRACION

Integrar es el proceso recíproco de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x). Se dice, entonces, que F(x) es una primitiva o antiderivada de f(x); dicho de otro modo las primitivas de f(x) son las funciones derivables F(x) : F(x) = f(x).

Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en una constante. La integral indefinida se representa por: ∫ f (x)dx