a Carla Salazar 5 éve
898
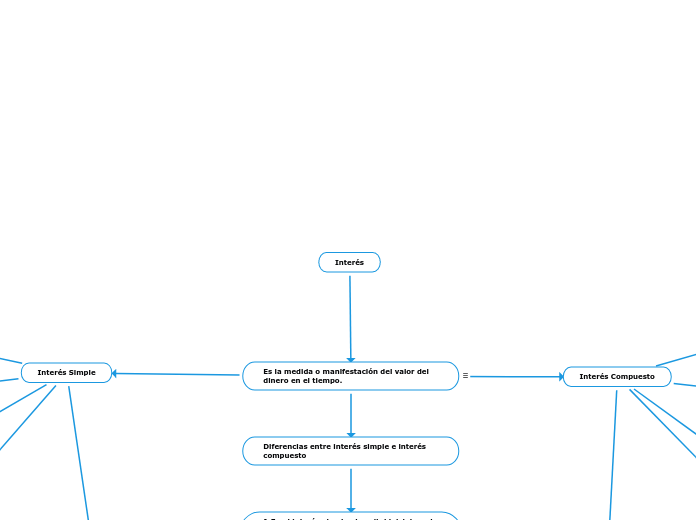
Interés
a Carla Salazar 5 éve
898

Még több ilyen
Referencia.
Meza, J. (2011). Matemáticas financieras Aplicadas. Ecoe ediciones. Disponible en https://bit.ly/2D3Iftg
2. En el interés simple el interés es el mismo, mientras en el interés compuesto el interés va variando en cada periodo.
F=P(1 + i)n
se aplica la tasa de interés sobre el monto inicial y también sobre los intereses que se van ganando cada período
VF = VP x (1 + r)n
En donde, VF= valor futuro VP= valor presente (el monto que invertimos hoy para ganar intereses) r= tasa de interés simple n= número de períodos
Proceso mediante el cual los intereses que se van causando periódicamente se suman al capital anterior
Períodos de capitalización: Diario: cuando al final de cada día los intereses generados se suman al capital. Mensual: indica que al final de cada mes se suman los intereses al capital anterior.
3. Los intereses periódicos siempre serán mayores.
2. La tasa de interés siempre se aplica sobre un capital diferente.
1. El capital inicial cambia en cada período porque los intereses que se causan se capitalizan, o sea, se convierten en capital.
También interés sobre interés, es aquel que al final del período capitaliza los intereses causados en el período inmediatamente anterior. En el interés compuesto el capital cambia al final de cada período, debido a que los intereses se adicionan al capital para formar un nuevo capital sobre el cual se calculan los intereses.
Ocurre cuando se aplica la tasa de interés solo sobre el capital o monto inicial, no sobre los intereses que se van ganando en el tiempo.
VF = VP x (1 + r x n)
En donde: VF= valor futuro VP= valor presente (el monto que invertimos hoy para ganar intereses) r= tasa de interés simple n= número de períodos
se basa en la determinación futura de un capital utilizando una fórmula no acumulativa. Es decir, el capital inicial genera unos intereses, pero estos no se añaden a dicha cuantía para calcular sus rendimientos futuros. En otras palabras: los rendimientos siempre se generan en base al capital original. Se puede utilizar en inversiones o cuando un préstamo está en fase de carencia, es decir, cuando solo se pagan los intereses. La fórmula se aplica fundamentalmente en inversiones con una duración igual o inferior a un año (a corto plazo). Sin embargo, el periodo se puede extender durante más tiempo.
Formula
I= C0 x Ti x t
En donde: I = Intereses obtenidos. CO = Capital Inicial Ti = Tasa de Interés t = Tiempo de inversión
I= K P n
En donde: I = Valor de interés K = Constante de proporcionalidad P = Capital n = Tiempo
3. Por la misma razón, puede decirse que los intereses serán siempre iguales en cada período, o menores si hay abonos al capital principal.
2. Como consecuencia de la característica anterior, la tasa de interés siempre se aplicará sobre el mismo capital, es decir, sobre el capital inicial o sobre el capital insoluto.
1. El capital inicial no varía durante todo el tiempo de la operación financiera ya que los intereses no se capitalizan. Esta condición se cumple siempre que no se haga abono al capital principal. En caso de pagos sobre el capital inicial, los intereses se calcularán sobre el capital insoluto.
Se llama interés simple aquél en el cual los intereses devengados en un período no ganan intereses en los períodos siguientes, independientemente de que se paguen o no. Únicamente sobre el capital principal se liquidan los intereses sin tener en cuenta los intereses precedentes causados. La liquidación de los intereses se hace sobre el saldo insoluto, es decir, sobre el capital no pagado.