a roman lewis 3 éve
213
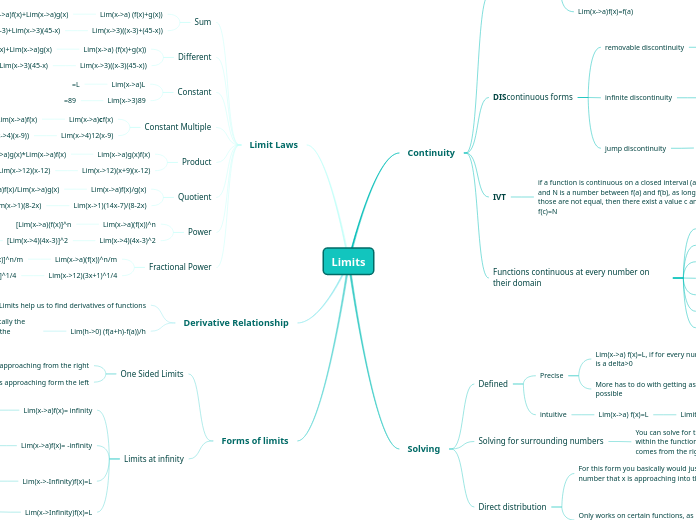
Limits
a roman lewis 3 éve
213

Még több ilyen
f(x) comes really close to L as it becomes significantly larger, creating a horizontal asymptote at y=L
f(x) comes really close to L as it becomes significantly more negative, creating a horizontal asymptote at y=L
creates a vertical asymptote at x=a as the values surrounding a, become significantly negative as it approaches a
creates a vertical asymptote at x=a as the values surrounding a, become significantly larger as it approaches a
Lim(x->a-)f(x)
Limit of f(x) as x approaches a from the left
Lim(x->a+)f(x)
Limit of f(x) as x approaches a from the right
[Lim(x->12)(3x+1)]^1/4
(37)^1/4=2.466
[Lim(x->a)(f(x)]^n/m
[Lim(x->4)(4x-3)]^2
(13)^2=169
[Lim(x->a)(f(x)]^n
Lim(x->1)(14x-7)/Lim(x->1)(8-2x)
=7/6
Lim(x->a)f(x)/Lim(x->a)g(x)
Lim(x->12)(x+9)*Lim(x->12)(x-12)
21*0=0
Lim(x->a)g(x)*Lim(x->a)f(x)
12(Lim(x->4)(x-9))
12(-5)=-60
c(Lim(x->a)f(x)
=89
=L
Lim(x->3)(x-3)-Lim(x->3)(45-x)
Lim(x->3)(x-3)+Lim(x->3)(45-x)
0+42=42
Lim(x->a)f(x)+Lim(x->a)g(x)
Transcendental
Lim(x->a)2^x=2^a
Lim(x->3)2^x=2^3
=8
Trig Functions
Lim(x->a)cosx=cosa
Lim(x->0)cosx=cos(0)
=1
Rational
Lim(x->a)1/x-3=1/a-3
Lim(x->8)1/x-3=1/8-3
=1/5
Polynomial
Lim(x->a)x^2-3x+1=a^2-3a+1
Lim(x->4)x^2-3x+1=4^2-3(4)+1
16-12+1=5
if Lim(x->3)f(x)
solve for x=2.9999, x=3.001
Lim(x->a) f(x)=L
Limit of f(x) as x approaches a is L
More has to do with getting as close to the value as possible
Epsilon, along y-axis
room around the y value
Delta, along x-axis
How much room around that x value
Lim(x->a) f(x)=L, if for every number epsilon>0 there is a delta>0
if 0<|x-a|
limits form the left and right exist but are not the same
lim(x->a)f(x)=DNE
funtion goes to infinity or -infinity at a
lim(x->a)f(x)=infinity (not a real number)
f(a)= may be defined
vfff
we can redefine F(x) at a just as a single value
Lim(x->a)f(x)does not = f(a)
f(a)=DNE
lim(x->a)f(x)=L