a Igal Brener 6 éve
687
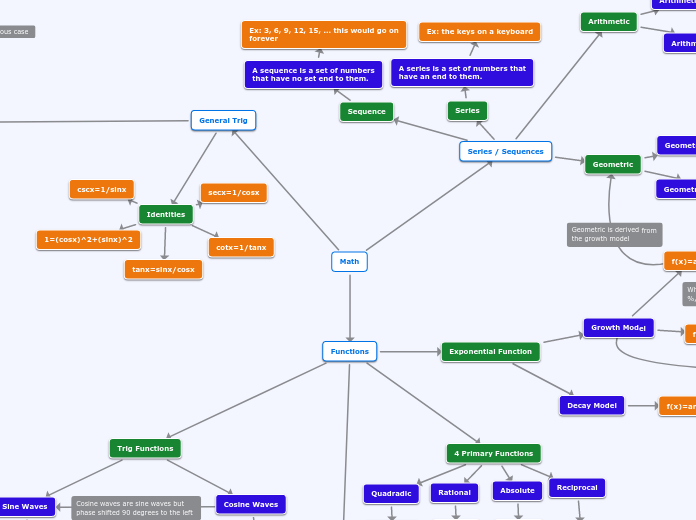
Math
a Igal Brener 6 éve
687

Még több ilyen
Sn=a(r^n-1)/r-1
ar^n-1
a+d(n-1)
Sn=n(2a+d(n-1))/2
Sn=n(a+tn)/2
Ex: 3, 6, 9, 12, 15, ... this would go on forever
Ex: the keys on a keyboard
This is the CAST rule
Angles for 45°
Angles for: 30° and 60°
h=asinB
A function where numbers can be any value within a set.
Ex: time it took to complete some task at any point you could say 1/2 of a second, 1 microsecond, 1 minute but there is a defined set if the task for example took 10 minutes.
tn=t(n-1)....
A function that calls upon previous numbers within the function.
Ex: the Fibonacci sequence that uses the previous numbers in the sequence to make the new number.
A function that has specific data set. Aka: several points in data.
Ex: # of students in a class, only a set # as you cannot have 1/2 of a student.
f(x)=A₀(1+i)^x
f(x)=ar^x
f(x)=ar^x (where r is a decimal / fraction)
f(x)=1/x
f(x)=|x|
f(x)=√x
f(x)=x^2
f(x)=acos(k(x-h))+c
f(x)=asin(k(x-h))+c
(x,y)---}((x/k)+h,ay+c)