Organigrama

Még több ilyen

Aplicaciones de la derivada al análisis de funciones

Szerző: Yolima Viasus Perez

La Derivada

Szerző: Yuston Lopez Garcia

MAPA MENTAL DE LA CIRCULACION

Szerző: alejandro torres

Líquidos corporales

Szerző: Luciana Baquero

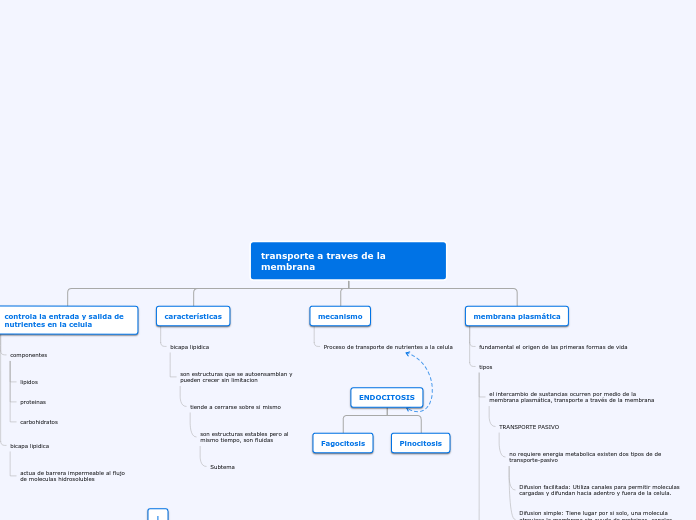
Pasivo

Difusion facilitada

Solo pasan moleculas especificas

osmosis

El disolvente pasa selectivamente a traves de la membrana celular

Hipotonica

Mayor concentracion dentro de la celula

Hipertonica

Mayor concentracion de agua afuera de la celula

Isotonica

Igual concentracion dentro y fuera de la celula

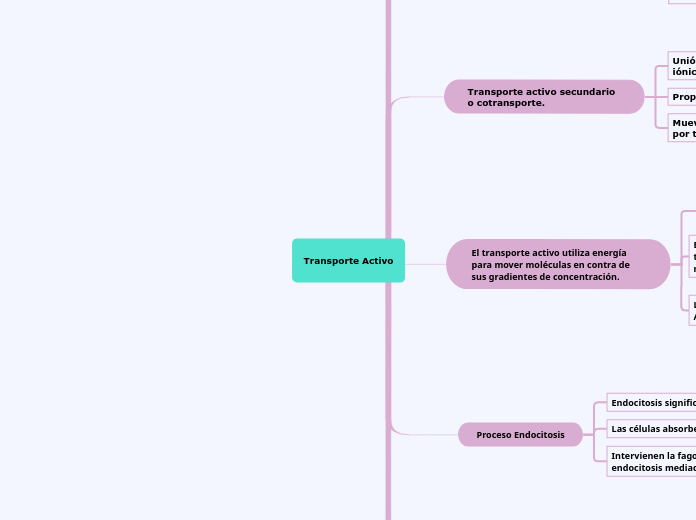
Activo

Exocitosis

Salida de moleculas grandes desde el interior de la celula

Endocitosis

La celula obtiene materiales que no pueden pasar a traves de la memebrana

Transporte celular

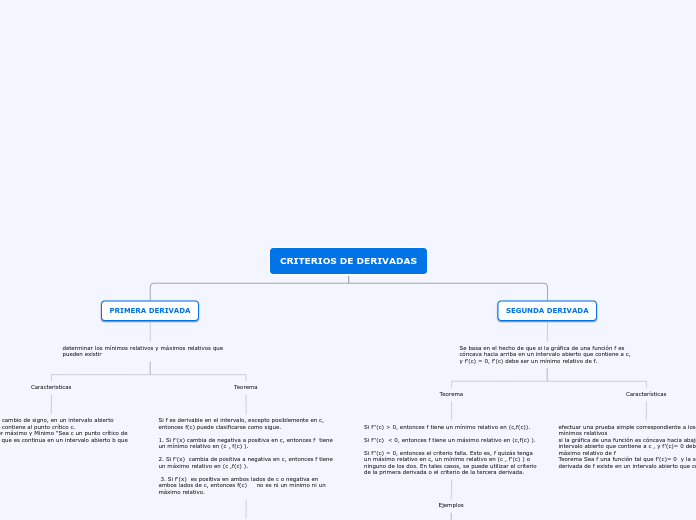
CRITERIOS DE DERIVADAS

SEGUNDA DERIVADA

Se basa en el hecho de que si la gráfica de una función f es cóncava hacia arriba en un intervalo abierto que contiene a c, y f'(c) = 0, f'(c) debe ser un mínimo relativo de f.

Características

efectuar una prueba simple correspondiente a los máximos y mínimos relativos si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a c , y f'(c)= 0 debe ser un máximo relativo de f Teorema Sea f una función tal que f'(c)= 0 y la segunda derivada de f existe en un intervalo abierto que contiene a c 1.

Si f''(c) > 0, entonces f tiene un mínimo relativo en (c,f(c)). Si f''(c) < 0, entonces f tiene un máximo relativo en (c,f(c) ). Si f''(c) = 0, entonces el criterio falla. Esto es, f quizás tenga un máximo relativo en c, un mínimo relativo en (c , f'(c) ) o ninguno de los dos. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.

PRIMERA DERIVADA

determinar los mínimos relativos y máximos relativos que pueden existir

Teorema

Si f es derivable en el intervalo, excepto posiblemente en c, entonces f(c) puede clasificarse como sigue. 1. Si f'(x) cambia de negativa a positiva en c, entonces f tiene un mínimo relativo en (c , f(c) ). 2. Si f'(x) cambia de positiva a negativa en c, entonces f tiene un máximo relativo en (c ,f(c) ). 3. Si f'(x) es positiva en ambos lados de c o negativa en ambos lados de c, entonces f(c) no es ni un mínimo ni un máximo relativo.

Ejemplos

Caracteristicas

se observa el cambio de signo, en un intervalo abierto señalado que contiene al punto crítico c. Teorema Valor máximo y Mínimo "Sea c un punto crítico de una función f que es continua en un intervalo abierto b que contiene a c.